По таблице из трех узловых точек
По таблице из трех узловых точек
можно построить интерполяционный полином Лагранжа второго порядка вида:
1. 0; 2. 0.5; 3. 1; 4. 0.4; 5. 0.35.
По таблице из трех узловых точек
найти табличные разности первого порядка 1. 2. 3. 4. 5.
По таблице из трех узловых точек
найти табличную разность второго порядка 1. 2. 3. 4. 5.
16. Какое из приведенных ниже понятий не используется в теории численного интегрирования? 1. квадратурные и кубатурные формулы; 2. квадратурная формула Ньютона-Котеса; 3. коэффициенты Котеса; 4. достаточные условия сходимости; 5. формула Симпсона.
17. Как называется частный случай квадратурной формулы Ньютона-Котеса при 1. формула Ньютона; 2. формула Котеса; 3. формула трапеций; 4. формула Симпсона; 5. формула Эйлера.
18. Как называется частный случай квадратурной формулы Ньютона-Котеса при 1. формула Ньютона; 2. формула Котеса; 3. формула трапеций; 4. формула Симпсона; 5. формула Эйлера.
19. Как называется следующая квадратурная формула: 1. формула Ньютона-Котеса; 2. формула трапеций; 3. формула Симпсона; 4. формула Ньютона; 5. формула Котеса.
20. Как называется следующая квадратурная формула: 1. формула Ньютона-Котеса; 2. формула трапеций; 3. формула Симпсона; 4. формула Ньютона; 5. формула Котеса.
21. Как называются коэффициенты вида: 1. коэффициенты Лагранжа; 2. коэффициенты Ньютона; 3. коэффициенты Ньютона-Котеса; 4. коэффициенты Котеса; 5. коэффициенты Симпсона.
22. Как называется следующая квадратурная формула: 1. формула Котеса; 2. формула Ньютона-Котеса; 3. формула Симпсона; 4. формула трапеций; 5. формула Ньютона.
23. Как называются величины 1. табличные разности первого порядка; 2. табличные разности второго порядка; 3. табличные разности различных порядков; 4. равноотстоящие узловые точки; 5. неравноотстоящие узловые точки.
24. Как называется величина 1. табличные разности первого порядка; 2. табличные разности второго порядка; 3. табличные разности различных порядков; 4. равноотстоящие узловые точки; 5. неравноотстоящие узловые точки.
25. Как называется величина 1. табличные разности первого порядка; 2. табличные разности второго порядка; 3. табличные разности различных порядков; 4. равноотстоящие узловые точки; 5. неравноотстоящие узловые точки.
26. Какие понятия используются в задаче аппроксимации? 1. отклонение построенной функции от экспериментальной; 2. узловые точки; 3. полином 4. коэффициенты полинома; 5. все ответы правильные.
27. Какие понятия используются в теории численного интегрирования? 1. однократные и двукратные интегралы; 2. квадратурные и кубатурные формулы; 3. квадратурные формулы Ньютона-Котеса, трапеций, Симпсона; 4. обобщенная кубатурная формула Симпсона; 5. все ответы правильные.
28. В чем состоит основная идея метода наименьших квадратов? 1.по заданной таблице значений построить приближенно функцию таким образом, чтобы построенная функция проходила через узловые точки; 2.по заданной таблице значений построить приближенно функцию таким образом, чтобы построенная функция не проходила через узловые точки; 3.по заданной таблице значений построить приближенно функцию таким образом, чтобы построенная функция могла как проходить через узловые точки, так и не проходить через них; 4.по данным эксперимента построить приближенно функцию таким образом, чтобы сумма квадратов отклонений построенной функции от экспериментальной в узловых точках была минимальна; 5.по данным эксперимента построить приближенно функцию таким образом, чтобы сумма отклонений построенной функции от экспериментальной в узловых точках была минимальна.
29. В каком пункте алгоритма метода наименьших квадратов допущена ошибка? 1. Задается таблица чисел 2. Вводится функция 3. Находятся необходимые условия экстремума функции 4. Строится и решается СЛАУ относительно неизвестных коэффициентов 5. Записывается искомый многочлен в виде
30. В каком пункте алгоритма метода наименьших квадратов допущена ошибка? 1. Задается таблица чисел 2. Вводится функция 3. Находятся необходимые условия экстремума функции 4. Строится и решается СЛАУ относительно неизвестных коэффициентов 5. Записывается искомый многочлен в виде
31. В каком пункте алгоритма метода наименьших квадратов допущена ошибка? 1. Задается таблица чисел 2. Вводится функция 3. Находятся необходимые условия экстремума функции 4. Строится и решается система нелинейных уравнений относительно неизвестных коэффициентов 5. Записывается искомый многочлен в виде
32. Когда возникает задача численного дифференцирования? 1. необходимо знать значения производных в узловых точках для функций, заданных таблицей, или для функций, имеющих сложный аналитический вид; 2. необходимо знать значения функции между узловыми точками; 3. необходимо знать значения функции в точках, расположенных в начале или в конце таблицы; 4. необходимо представить в аналитическом виде функцию, заданную таблично; 5. необходимо представить в более простом виде сложную аналитически заданную функцию.
33. Продолжите определение собственного интеграла: «Интеграл вида 1. промежуток интегрирования 2. промежуток интегрирования 3. промежуток интегрирования 4. промежуток интегрирования 5. промежуток интегрирования
34. Продолжите определение несобственного интеграла: «Интеграл вида 1. промежуток интегрирования 2. промежуток интегрирования 3. промежуток интегрирования 4. промежуток интегрирования 5. промежуток интегрирования
35. В чем состоит принципиальное отличие теорий интерполяции и аппроксимации функций? 1. в задаче интерполяции искомый полином проходит через узловые точки; в задаче аппроксимации – не проходит через них; 2. в задаче интерполяции искомый полином проходит через узловые точки; в задаче аппроксимации – проходит на расстоянии, минимально удаленном от узловых точек; 3. в задаче интерполяции искомый полином не проходит через узловые точки; в задаче аппроксимации – проходит; 4. в задаче интерполяции искомый полином не проходит через узловые точки; в задаче аппроксимации – проходит на расстоянии, минимально удаленном от узловых точек; 5. принципиальных отличий нет.
36. Когда возникает задача численного интегрирования? 1. необходимо знать значения функции между узловыми точками; 2. необходимо знать значения функции для точек, расположенных в начале или в конце таблицы; 3. необходимо представить в аналитическом виде функцию, заданную таблицей; 4. необходимо представить в более простом виде сложную аналитически заданную функцию; 5. необходимо вычислить определенный интеграл от функций, заданных таблицей, или от функций, имеющих сложный аналитический вид.
|

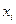
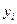
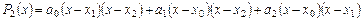 . Чему будет равен коэффициент
. Чему будет равен коэффициент 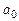 ?
? и
и 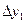 .
.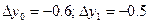 ;
;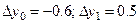 ;
;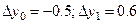 ;
; ;
;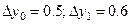 .
.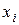
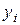
 .
.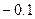 ;
; ;
; ;
;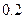 ;
; .
. ?
?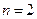 ?
?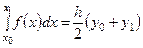 ?
?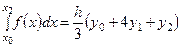 ?
? ,
, 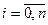 , используемые в теории численного интегрирования?
, используемые в теории численного интегрирования?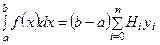 ?
?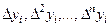 , используемые в теории интерполирования функций?
, используемые в теории интерполирования функций? , используемая в теории интерполирования функций?
, используемая в теории интерполирования функций?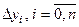 , используемая в теории интерполирования функций?
, используемая в теории интерполирования функций?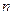 -й степени;
-й степени;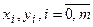 .
. , где
, где  - отклонение функции от экспериментальной в узлах
- отклонение функции от экспериментальной в узлах 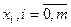 .
. .
.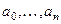 ;
; .
. , где
, где 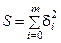 , где
, где 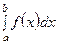 называется собственным, если:
называется собственным, если: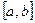 конечен и подынтегральная функция
конечен и подынтегральная функция  разрывна на
разрывна на 


