Середина. Привязка к ближайшему концу (конечной точке) объекта.

Конточка

Привязка к ближайшему концу (конечной точке) объекта.

Выберите этот тип привязки, а все остальные отключите. Начертите отрезок. Затем еще раз нажмите инструмент Отрезок так, как будто хотите начертить второй отрезок. Курсор мыши наведите на любую точку первого отрезка. Вы увидите значок — квадрат и надпись Конточка на конце первого отрезка. Наш новый отрезок согласно объектной привязке будет начинаться из этой точки.

Середина

Привязка к середине объекта на чертеже.

Начертите отрезок, затем выберите привязку Середина, а все остальные – отключите. Теперь наведите курсор на ваш отрезок. Вы увидите значок — треугольник с надписью Середина по центру отрезка. Если вы захотите начертить другой отрезок, то он будет начинаться именно в этой точке.

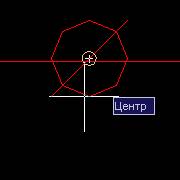
Центр

Привязка к центру окружности, дуги или эллипса.

Выберите привязку Центр. Начертите окружность, а затем нажмите на инструмент Отрезок. Курсор мыши наведите на окружность. Вы увидите надпись Центр и значок привязки – круг. Если вы начертите отрезок, он будет выходить из центра окружности.

Узел

В официальном описании AutoCAD этой привязке дается следующее определение:

Привязка к объекту-точке, определяющей точке размера или начальной точке размерного текста.

Но на практике часто это просто привязка к точкам сетки. Если вы выбрали привязку Узел, то новый отрезок или многострочный текст сможете вставить только на местро точки (узла) сетки – то есть выровнять объект по сетке. Это часто пригождается на практике.

Если ваш отрезок был разбит на узлы при помощи инструмента Точка, то привязка Узел поможет чертить новые объекты из центра узлов (точек).