Примеры решения задач. Задача 1. Найти координаты векторного произведения , если , .Задача 1. Найти координаты векторного произведения Решение. Найдем Задача 2. Силы
Решение. Найдем силу сил
Задача 3. Даны координаты вершин параллелепипеда: Решение. По определению, объем параллелепипеда равен смешанному произведению векторов, на которых он построен. Найдем эти векторы:
Объем этого параллелепипеда С другой стороны, объем параллелепипеда
Угол между вектором и гранью
так как вектор
Итак: Задача 4. Проверить, лежат ли в одной плоскости точки Решение. Найдем три вектора:
Три вектора лежат в одной плоскости, если они компланарны, т. е. их смешанное произведение равно нулю:
Решая эту систему, получим
|
, если 
, 
.
и 
. Векторное произведение, по определению, равно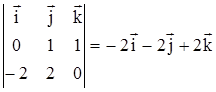 
.
и 
приложены к точке 
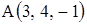. Вычислить величину момента равнодействующей этих сил 
относительно точки 
.
: 
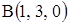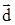. Момент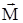
вычисляется по формуле
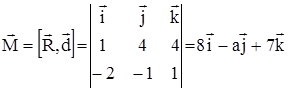, а его модуль 
.
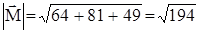. Найти объем параллелепипеда, его высоту, опущенную из вершины С, угол между вектором AD и гранью, в которой лежат векторы АВ и АС.
.
.
, 
- это площадь параллелограмма: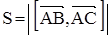 
.
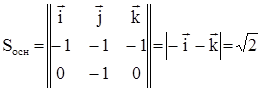, тогда высота 
.
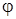найдем по формуле
.
перпендикулярен грани, в которой лежат векторы 
. Угол между этим вектором и вектором 
находим по известной формуле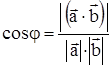
. Очевидно, что искомый угол 
.
.
, 
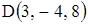. Найти линейную зависимость вектора 
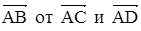, если это возможно.
.
.
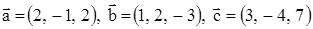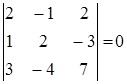. Следовательно, эти три вектора линей-
но зависимы. Найдем линейную зависимость 
от 
.
.
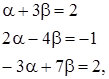, т.е.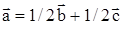 
.
