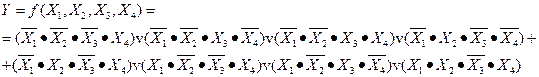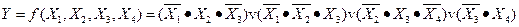Задание 1. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ «ГОРНЫЙ»
Кафедра электронных систем
Контрольная работа ПО ДИСЦИПЛИНЕ «Вычислительная и микропроцессорная техника» Выполнила студентка: Тарасова Юлия Валерьевна
Подпись: \ ______________\
Проверил преподаватель: Борисов Сергей Викторович
Группа: ММОз-11б
Номер студенческого билета: 1120030049
Дата сдачи:
Санкт-Петербург 2015 г.
Содержание
Задание 1 ………………………………………………………………………………………...… 2
Задание 2 …………………………………………………………………………………...…...…. 6
Литература ……………………………………………………………………………...…………10
Задание 1
Логическая функция четырёх булевых переменных X1, X2, X3, X4 имеет истинное значение на тех наборах входных переменных, которые эквивалентны десятичным числам: 1; 2; 3; 4; 5; 9; 10;13. Требуется: 1) Построить таблицу истинности для полного набора функций четырёх указанных переменных и определить из неё СДНФ, удовлетворяющую условиям задачи; 2) Минимизировать полученную функцию графическим методом Карно-Вейча или табличным - Квайна МакКласки; 3) На основании полученной тупиковой формы переключательной функции построить логическую схему на интегральных микросхемах (ИМС) средней степени интеграции.
Решение:
1) Таблица 1. Таблица истинности для полного набора функций 4-х переменных.
Для записи совершенной дизъюнктивной нормальной формы (СДНФ) переменных, удовлетворяющей условиям задачи:
А) Выпишем строки, в которых Y = 1: 1) Х1 = 0; Х2 = 0; Х3 = 0; Х4 = 1; Y = 1; 2) Х1 = 0; Х2 = 0; Х3 = 1; Х4 = 0; Y = 1; 3) Х1 = 0; Х2 = 0; Х3 = 1; Х4 = 1; Y = 1; 4) Х1 = 0; Х2 = 1; Х3 = 0; Х4 = 0; Y = 1; 5) Х1 = 0; Х2 = 1; Х3 = 0; Х4 = 1; Y = 1; 6) Х1 = 1; Х2 = 0; Х3 = 0; Х4 = 1; Y = 1; 7) Х1 = 1; Х2 = 0; Х3 = 1; Х4 = 0; Y = 1; 8) Х1 = 1; Х2 = 1; Х3 = 0; Х4 = 1; Y = 1. Б) Запишем эти строки в виде конъюнкции (операции «И») аргументов. Если аргумент равен «0», он записывается с инверсией, а если «1», то без инверсии:
- объединим все произведения переменных (минтермы) с помощью дизъюнкции:
Полученное выражение является СДНФ, так как минтермы объединены с помощью дизъюнкции, причём в каждый минтерм входят все переменные. Каждая функция имеет единственную СДНФ.
2) Чтобы минимизировать полученную функцию до минимальной дизъюнктивной нормальной формы (МДНФ) графическим методом Карно:
А) Построим карту Карно-Вейча для функции 4-х переменных:
Б) Если какой-то из этих минтермов в СДНФ присутствует, то в соответствующей клетке ставится «1»; если какого-либо минтерма нет, то проставляется «0»; при этом переменная без инверсии считается за «1», а с инверсией - за «0». В) Объединяем ячейки таблицы: - все области должны быть прямоугольными или квадратными; - в каждой области может быть 1, 2, 4, 8 клеток, то есть количество клеток в области должно быть равно числу 2 в целой неотрицательной степени; - области должны быть как можно больше; - карту Карно можно сворачивать в цилиндр по вертикали или по горизонтали; - одна клетка может входить в две и более области. - не нужно создавать лишние области, то есть, если все клетки уже вошли в области, больше областей не нужно; - при минимизации СДНФ в области объединяются единицы; - при минимизации СКНФ в области объединяются нули.
С) Производится анализ переменных в каждой области: - если переменная равна 1, она записывается без инверсии; - если переменная равна 0, она записывается с инверсией; - если переменная изменяется, она сокращается; - записываются минтермы, в которых переменные объединяются знаками конъюнкции (операция «И»); - минтермы объединяются знаками дизъюнкции (операция «ИЛИ»); - получается МДНФ.
3) На основании полученной тупиковой формы переключательной функции построим логическую схему. Для нашей МДНФ эта схема будет следующей:
Рисунок 1. Логическая схема для МДНФ.
Рассматривая возможность построения данной схемы на ИМС средней степени интеграции, и руководствуясь справочником [2], выберем ИМС: К555ЛН1 - 1 шт.; К555ЛЛ1 - 2 шт. и К555ЛИ1 - 1 шт. Выбор данных ИМС был произведён по перечню справочника [2] Используя данные ИМС, можно реализовать работу логической схемы нашей МДНФ (рис.1) в практическом использовании.
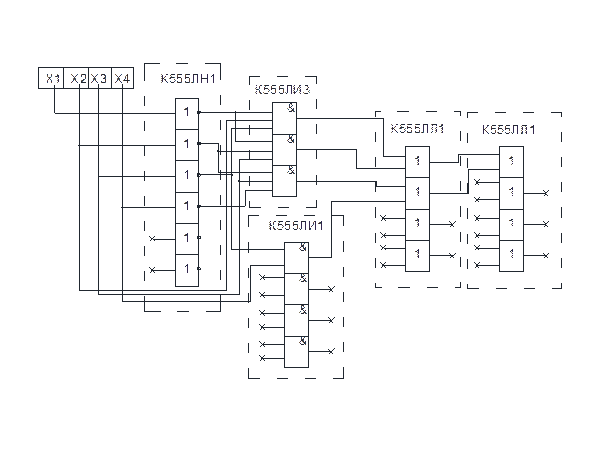
Приблизительная схема реализации нашей функции на данных ИМС будет иметь структуру, указанную на рис.2.
Рисунок 2. Логическая схема реализации МДНФ на выбранных ИМС.
|