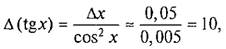Пример 6. Пример 7. Пусть в приближенном значении а = 16,395 все цифры верны в широком смысле
Пример 8. Пусть х = 984,6; δх = 0,008. Очевидно, что 0,008 ≤1·10-2. Это означает, что число х имеет по крайней мере одну верную в строгом смысле цифру (это первая слева цифра 9). Полученный результат легко подтвердить, используя определение цифры, верной в строгом смысле. Вычислим: х = 984,6·0,008 = 7,8768, откуда следует, что в числе 984,6 цифра 9 действительно верна в строгом смысле. Пример 9. Пусть х = 136,4; δх = 0,008 ≤1·10-2 (т.е. п = 2). Согласно правилу в числе 136,4 лишь одна верная в строгом смысле цифра (n - 1 = 1). Вычислим Δх = 136,4 · 0,008 < 1,1. Как показывает найденная величина предельной абсолютной погрешности, в числе 136,4 верны в строгом смысле две цифры: 1 и 3. Пример 10. Пусть х = 78,56; δх = 0,0003. Имеем 0,0003 < 0,0005 = Пример 11. Даны приближенные значения х = 235,4 и у = 79,1834, у которых все цифры являются верными в широком смысле. Найдем на МК их сумму: S= 235,4 + 79,1834 = 314,5834. Для оценки точности результата вычислим сумму погрешностей слагаемых: 1·10-1+1·104 =0,1001 < 0,2 = Δs. Величина ошибки показывает, что в результате уже первый знак после запятой является сомнительным. Стоило ли терять время на учет в вычислениях всех знаков после запятой у второго слагаемого? Пример 12. Числа 43,1 и 5,72 заданы верными цифрами. Найдем на МК их частное q=7,534965. Для определения числа верных знаков результата вычислим
Частное q имеет один верный знак (7). Округляя полученный результат с одной запасной цифрой, получим q = 7,5. Пример 13. С помощью МК получаем sin 0,8 = 0,717356091. Если 0,8 — точное значение, то в соответствии с точностью вычислительного прибора полученный результат имеет точность ±1 • 10-9. Если же 0,8 — приближенное значение, у которого цифра 8 верна, например, в строгом смысле, то предельная абсолютная погрешность значения аргумента Δх = 0,05, а погрешность полученного значения синуса в соответствии с формулой оценки предельной абсолютной погрешности будет Δ(sinx) = cosх·Δх ≤ 0,7 ·0,05 = 0,035. Отсюда следует, что во втором случае полученное на МК значение sin 0,8 = 0,717356091 имеет лишь одну верную значащую цифру. Округляя результат с одной запасной цифрой, получим 0,72. Пример 14. Пусть х= 1,5, причем Δх = 0,05, т.е. все цифры в числе х верны в строгом смысле. Нужно вычислить значение tgx. С помощью МК получаем: tg 1,5 = 14,10141994. Для определения верных цифр в результате оценим его абсолютную погрешность: отсюда следует, что в полученном значении tg 1,5 ни одну цифру нельзя считать верной. Пример 15. Значение аргумента х=0,63 имеет относительную ошибку около 0,1%. Оценить величину относительной ошибки sin 0,63. Используя соответствующую формулу, с помощью МК получим: δ (sin0,63) = |0,63·ctg0,63| ·0,001 ≈0,000864 ≈ 0,08%. Используя величину найденной относительной погрешности, можно оценить количество верных в строгом смысле значащих цифр в искомом значении sin 0,63. Поскольку имеет место 0,00864 < 1 • 10 -3, то можно сделать вывод, что в значении sin 0,63 = 0,589145 по крайней мере две цифры после запятой верны в строгом смысле. Пример 16.
Пример 17.
|

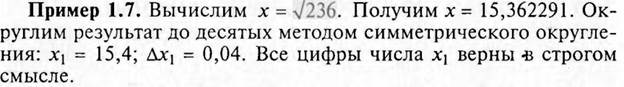 Пример 7. Пусть в приближенном значении а = 16,395 все цифры верны в широком смысле. Округлим а до сотых: а1 = 16,40. Погрешность округления Δокр = 0,005. Для нахождения полной погрешности Δа1 нужно сложить Δокр с погрешностью исходного значения а1, которая в данном случае может быть найдена из условия, что все цифры и записи а верны: Δа = 0,001. Таким образом, Δа1 = 0,001 + 0,005 = 0,006. Отсюда следует, что в значении а1δ = 16,40 цифра 0 не верна в строгом смысле.
Пример 7. Пусть в приближенном значении а = 16,395 все цифры верны в широком смысле. Округлим а до сотых: а1 = 16,40. Погрешность округления Δокр = 0,005. Для нахождения полной погрешности Δа1 нужно сложить Δокр с погрешностью исходного значения а1, которая в данном случае может быть найдена из условия, что все цифры и записи а верны: Δа = 0,001. Таким образом, Δа1 = 0,001 + 0,005 = 0,006. Отсюда следует, что в значении а1δ = 16,40 цифра 0 не верна в строгом смысле. • 10-3 т.е. в числе х верны в строгом смысле три цифры. Действительно, в данном случае Δх = 78,56 • 0,0003 < 0,03, что подтверждает полученный результат.
• 10-3 т.е. в числе х верны в строгом смысле три цифры. Действительно, в данном случае Δх = 78,56 • 0,0003 < 0,03, что подтверждает полученный результат.