Примеры рядов.
Атрибутивный ряд:
Дискретный вариационный ряд:
Интервальный ряд:
При необходимости интервальные ряды представляют в дискретном виде, для этого переходят к серединам интервалов:
В зависимости от характера распределения единиц совокупности интервалы могут быть равными или неравными, открытыми или закрытыми, ограниченными или неограниченными.
Интервалы неравные, крайние интервалы открытые, правый крайний интервал неограниченный; левый крайний интервал ограничен нулем. Если число наблюдений (n) небольшое, то варианты достаточно просто ранжировать, т. е. расположить в порядке возрастания их значений. Например, при измерении размеров вируса орнитоза получены следующие величины (в мкм): 0,34; 0,45; 0,20; 0.29; 0,40. Эти варианты нужно записать в такой последовательности: 0,20; 0,29; 0,34; 0,40; 0,45. При увеличении числа наблюдений обычно отмечаются повторения отдельных вариант. В этом случае для построения вариационного ряда необходимо выписать все значения вариант в порядке возрастания, а затем подсчитать число повторений (частоту – Например, исследователем произведено 47 измерений мембранного потенциала мышечной клетки в покое (с точностью до 1 мВ). Составленный вариационный ряд показан в табл.3.1. Таким образом, главными составными элементами вариационного ряда являются: x – варианты - значения варьирующего признака; p – частоты - число повторений каждой варианты; n – общее число наблюдений (n равно сумме частот, т. е. n =Σ p). Последовательное суммирование частот образует так называемые накопленные частоты. Последняя накопленная частота представляет собой общее число наблюдений. Подобным же образом составляется и интервальный вариационный ряд, в котором перечисляются не отдельные варианты, а их группы. Таблица 3.1. – Результаты измерения потенциала мышечной клетки
Интервальный вариационный ряд следует составлять в тех случаях, когда исследователь имеет дело с большим разнообразием значений вариант (более 20). Интервалы в таком вариационном ряду целесообразно иметь одинаковыми, т. е. они должны объединять равное число значений вариант. Интервальные вариационные ряды строятся при изучении как дискретных величин (признаков, выражаемых только целым числом, например число посещений, операций, число эритроцитов, частота пульса и т. д.) так и при исследовании непрерывных величин (признаков, регистрируемых дробными числами, например, рост, вес, биохимические показатели т. п.). Для графического изображения рядов используют полигон (дискретный ряд) или гистограмму (интервальный ряд).
17. Основные направлениях анализа вариационного ряда.
В результате сводки материала получаются абсолютные числа, которые применяются в анализе для характеристики объема, размера явления (число больниц, число коек, число больных, бюджет здравоохранения и т. д.). При малых числах наблюдений, когда не требуется выявление закономерностей, тоже могут быть использованы абсолютные числа. Однако в большинстве случаев для анализа полученных данных необходимо предварительно описать полученную статистическую совокупность с помощью ряда параметров. Начинается описание статистической совокупности с расчета и анализа обобщающих коэффициентов. В здравоохранении и медицине чаще всего для этой цели используются относительные величины и средние величины.
18. Показатели центральной тенденции ряда и их практическое применение.
|

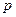 ) каждой варианты и записать их рядом с соответствующими значениями вариант.
) каждой варианты и записать их рядом с соответствующими значениями вариант.


