Проверка нормальности распределения
Соответствие экспериментального распределения нормальному проверяется следующими способами: 1. По числам Вестергарда при нормальном распределении в пределах: х ± 0.3σнаходится 25 % всех единиц наблюдения; х ± 0.7 σнаходится 50 % всех единиц наблюдения; х ± l,lσнаходится 75 % всех единиц наблюдения; х ± 3,0σнаходится 99 % всех единиц наблюдения. 2. По соотношению средней арифметической и структурных средних: - при нормальном распределении, которое обладает симметричностью:
а). если распределение симметрично: Me = Mo; б). если распределение обладает правосторонней асимметрией: Me > Mo; в). если распределение имеет левостороннюю асимметрией Me < Mo 3. По коэффициенту асимметрии (skewness):
б) при правосторонней асимметрии: в) при левосторонней асимметрии: 4. Если Ме занимает срединное положение между 25-м и 75-м процентилем, то распределение близко к нормальному. Графическое изображение симметричного и асимметричного распределений:
■гармоническое преобразование: ■извлечение квадратного корня: ■логарифмирование {дает наиболее точное приближение}: Успешность преобразования данных оценивают по коэффициенту асимметрии: чем ближе он к 0, тем ближе экспериментальное распределение к нормальному.
23. Правило исключения «выскакивающих» вариант.
Исключение "выскакивающих" вариант. Иногда в небольших совокупностях встречаются варианты резко отличающиеся по своему значению от других, так называемая «выскакивающая» варианта (outlying case). Если данное отличие обусловлено случайными колебаниями изучаемой величины, то такие варианты оставляют в совокупности и включают в общее число наблюдений. Если отличие обусловлено ошибками в исследовании или ее причину точно нельзя установить, то "выскакивающие" варианты необходимо исключить из исследования. Методика исключения вариант: 1. рассчитываются средняя величина и стандартное отклонение без учета "выскакивающих" вариант; 2. анализируется соотношение: – если – если При этом f - коэффициент Романовского, который определяется по специальной таблице с учетом числа наблюдений и вероятностью исключения варианты
24. Выборочное исследование и основные области его применения. Положительные и отрицательные стороны выборочного исследования.
Выборочное наблюдение - вид несплошного наблюдения, при котором отбор подлежащих обследованию единиц наблюдения из генеральной совокупности(population) осуществляется случайно, отобранная часть (выборка) (sample) подвергается обследованию, после чего результаты распространяются на всю исходную совокупность. Положительные стороны выборочного метода: – может быть единственно доступным способом сбора данных, если единицы наблюдения во время исследования подвергаются порче или уничтожению; – экономичность; – сжатые сроки исследования, что ускоряет получение результата; – большая точность получения результата за счет уменьшения случайных ошибок при сборе материала; – возможность задать надежность и точность исследования. Отрицательные стороны выборочного метода: – неизбежна ошибка в исследовании, связанная с тем, что не все единицы наблюдения подвергаются отбору; – может быть нежелательным, если по официальным предписаниям необходимо регистрировать каждую единицу наблюдения; – для редких событий малые выборки могут не накопить достаточного числа случаев; – при социологических исследованиях может вызвать чувство дискриминации у населения. Основное требование, предъявляемое к формированию выборки – случайность отбора единиц наблюдения из генеральной совокупности, при котором каждой единице наблюдения обеспечивается равная вероятность попадания в выборку (рандомизированный отбор) (randomization).
25. Выборка и ее репрезентативность.
Виды выборок: 1. В зависимости от способа отбора единиц наблюдения (от способа организации совокупности): – случайная: отбор единиц наблюдения производится непосредственно из генеральной совокупности. Случайность отбора достигается путем применения жеребьевки или использования таблицы случайных чисел. Различают бесповторную выборку и повторную (после регистрации единицы вновь возвращаются в генеральную совокупность) – механическая:генеральная совокупность разбивается на равные части, из которых затем в заранее обусловленном порядке отбирают единицы наблюдения под определенным номером (например, каждую пятую), так, чтобы обеспечить необходимое число наблюдений. Следует учитывать, что такой механический отбор не исключает возможности систематической ошибки. – типологическая (типическая):генеральная совокупность разбивается на качественно однородные по изучаемому признаку группы, а затем из этих групп производят случайный отбор необходимого числа единиц наблюдения. Объем выборки в каждой типической группе устанавливается пропорционально ее удельному весу в генеральной совокупности (пропорциональный отбор), а иногда и с учетом вариации в ней изучаемого признака (оптимальный отбор). – серийная (гнездовая):отбору подлежат не отдельные единицы наблюдения, а целые их группы (серии или гнезда), в составе которых единицы наблюдения связаны определенным образом: территориально (районы, селения и др.) или организационно (студенческие группы, больницы, предприятия и др.) и которые отбираются из генеральной совокупности по принципу случайного или механического отбора. Внутри серии производится сплошной отбор единиц наблюдения. - комбинированная 2. По этапам отбора: - одноступенчатая - многоступенчатая 3. В зависимости от числа программ отбора: - однопрограммная (однорядная) - многопрограммная (многорядная) Модификации видов выборок: - метод направленного отбора - метод парных выборок - когортный метод - метод моментного среза - Теоретическая основа выборочного метода - Взаимосвязь статистических показателей выборочной и генеральной совокупностей определяется законом больших чисел, выражаясь в теореме П. Л.Чебышева: чем больше число некоторых случайных величин, тем их средняя арифметическая ближе к средней арифметической генеральной совокупности, т.e. тем меньше разница между показателями выборочной и генеральной совокупностей. По мере увеличения числа наблюдений вероятность осуществления приближения показателя выборки к показателю генеральной совокупности становится все больше, стремясь к единице, если число на - Репрезентативность - это способность выборочной совокупности как количественно, так и качественно отражать свойства генеральной совокупности. Количественная репрезентативность достигается достаточностью числа наблюдений, качественная - соответствием признаков единиц наблюдения в выборочной и генеральной совокупностях.
26. Методы формирования выборки. Рандомизированный отбор.
Основное требование, предъявляемое к формированию выборки – случайность отбора единиц наблюдения из генеральной совокупности, при котором каждой единице наблюдения обеспечивается равная вероятность попадания в выборку (рандомизированный отбор) (randomization).
27. Оценка параметра генеральной совокупности и какие требования к ней предъявляются.
Любое значение параметра, вычисленное на основе ограниченного числа наблюдений, непременно содержит элемент случайности. Такое приближенное, случайное значение называется оценкой параметра. Оценка параметра должна быть доброкачественной, что определяется тремя факторами, которые дают наименьшие ошибки расхождения показателей выборочной и генеральной совокупностей: – состоятельность оценки, т.е. при увеличении числа наблюдений оценка параметра приближается к его значению в генеральной совокупности; – несмещенность оценки, т.е. при оценке отсутствуют систематические ошибки в сторону завышения или занижения параметра генеральной совокупности; – эффективность оценки, т.е. оценка должна обладать минимальной вариабельностью. Как правило, проводят точечную и интервальную оценку параметра.
28. Оценка достоверности результатов исследования и уровень его значимости. Выход результата за пределы доверительных границ в следствие случайных колебаний имеет незначительную вероятность. Пределы возможных отклонений, выраженные в долях где Существует таблица соответствия интеграла вероятности и значения
Таблица 1. Соотношения между доверительным коэффициентом, доверительной вероятностью и уровнем значимости При числе наблюдений больше 30 можно пользоваться следующей закономерностью: вероятности безошибочного прогноза
29. Точечная оценка параметра генеральной совокупности.
|

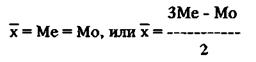
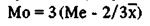

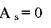
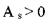
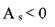

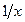 ;
;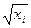 ;
;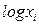
 , то "выскакивающая" варианта исключается из исследования;
, то "выскакивающая" варианта исключается из исследования;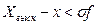 , то "выскакивающая" варианта должна быть оставлена в общем числе наблюдений.
, то "выскакивающая" варианта должна быть оставлена в общем числе наблюдений.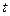 , оценивают по формуле:
, оценивают по формуле: 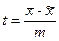 ;
; 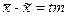 ;
; 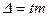 ,
,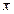 - среднее значение показателя в выборке,
- среднее значение показателя в выборке, 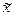 - среднее значение показателя в генеральной совокупности,
- среднее значение показателя в генеральной совокупности, 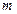 - ошибка репрезентативности,
- ошибка репрезентативности, 
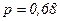 приблизительно соответствует
приблизительно соответствует  ; при
; при 
 , при
, при 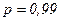
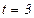 .
.


