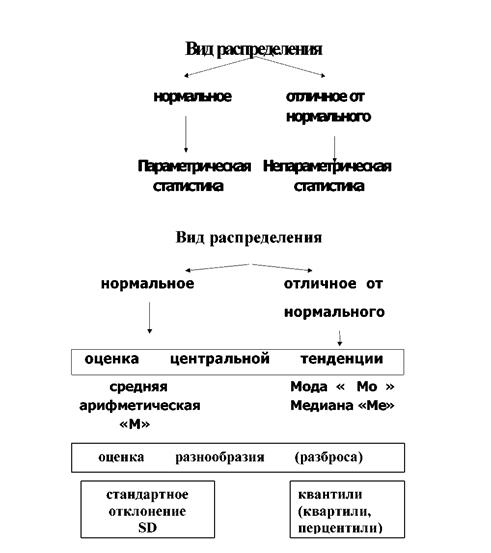
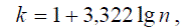Виды распределений
Нормальное (гауссово, симметричное, колоколообразное) распределение (normal, Gaussian distribution) - описывает совместное воздействие на изучаемое явление небольшого числа случайно сочетающихся факторов (по сравнению с общей суммой факторов), число которых неограничено велико. Встречается в природе наиболее часто, за что и получило название «нормального». Характеризует распределение непрерывных случайных величин.
р - вероятность появления данного значения в совокупности. Биномиальное распределение (распределение Бернулли) (binomial distribution, Bernoulli distribution) - описывает распределение частоты события, обладающего постоянной вероятностью появления при многократных испытаниях. При большом числе испытаний стремиться к нормальному. Крайним вариантом биномиального распределения является альтернативное распределение, при котором вся совокупность распределяется на две части (две альтернативы). Биномиальное распределение характеризует распределение дискретных случайных величин.
х - значения случайной величины; р - вероятность появления данного значения в совокупности.
15. Сравнительный анализ параметрической и непараметрической статистики.
Анализ совокупности начинается с установления вида распределения изучаемого признака. Для этого полученные данные представляются в виде вариационного ряда, изображаются графически и делаются соответствующие расчеты. В случае распределения близкого к нормальному мы вправе для дальнейшего статистического анализа применять параметрическую статистику, если распределение отлично от нормального или при неизвестном распределении рекомендуется применять непараметрическую статистику. Непараметрические методы: ■ не требуют предварительного знания вида распределения; ■ не требуют предварительного расчета параметров распределения (средних величин, стандартного отклонения и др.); ■ позволяют сравнивать совокупности с номинальными и порядковыми признаками; ■ просты в применении. Отрицательные стороны непараметрических методов: ■ обладают меньшей мощностью, чем параметрические; имеют существенные ограничения в применении по числу наблюдений
16. Вариационный ряд и правила его формирования. Примеры вариационных рядов
Вариационный ряд (frequency table) - ранжированный ряд распределения по величине какого-либо признака. Этот признак носит название варьирующего, а его отдельные числовые значения называются вариантами и обозначаются через " Вариационный ряд можно разбивать на отдельные (по возможности равные) части, которые называются квантилями (quantile). Наиболее часто употребляемые квантили представлены в таблице.
Рис 3.1. Этапы описания (обобщения) количественного признака
Виды вариационных рядов: 1. В зависимости от вида случайной величины: - дискретный; - непрерывный. 2. В зависимости от группировки вариант: - несгруппированный; - сгруппированный (интервальный): 3. В зависимости от частоты, с которой каждая варианта встречается в вариационном ряду: - простой (р =1); - взвешенный (р >1). При построении интервальных рядов могут возникнуть вопросы о числе групп и величине интервалов в группе. Для определения числа групп можно использовать формулу Стерджесса
где n – численность единиц (объем) изучаемой совокупности; k – число образуемых групп. Величина интервала вычисляется по формуле:
|

 х - значения случайной величины;
х - значения случайной величины;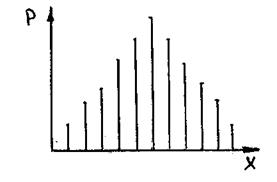 х - значения случайной величины; р - вероятность появления данного значения в совокупности.
х - значения случайной величины; р - вероятность появления данного значения в совокупности.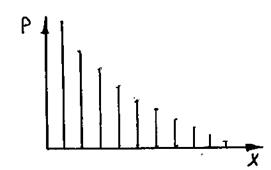 Распределение Пуассона – описывает события, при которых с возрастанием значения случайной величины, вероятность появления ее в совокупности резко уменьшается. Распределение Пуассона характерно для редких событий и может рассматриваться также как крайний вариант биномиального. Характеризует распределение дискретных случайных величин.
Распределение Пуассона – описывает события, при которых с возрастанием значения случайной величины, вероятность появления ее в совокупности резко уменьшается. Распределение Пуассона характерно для редких событий и может рассматриваться также как крайний вариант биномиального. Характеризует распределение дискретных случайных величин.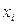 ". Число, показывающее, сколько раз данная варианта встречается в вариационном ряду, называется частотой и обозначается через "
". Число, показывающее, сколько раз данная варианта встречается в вариационном ряду, называется частотой и обозначается через "  "
"