1. При сопоставлении двух независимых серий наблюдений:
для частотных показателей: 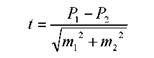
для средних величин: 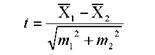
где 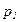 и
и 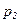 - частотные показатели в сравниваемых совокупностях;
- частотные показатели в сравниваемых совокупностях; 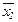 и
и 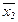 - средние величины в сравниваемых совокупностях;
- средние величины в сравниваемых совокупностях; 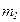 и
и  - ошибки репрезентативности показателей и средних величин в сравниваемых совокупностях.
- ошибки репрезентативности показателей и средних величин в сравниваемых совокупностях.
Для оценки достоверности полученного  - критерия при числе наблюдений больше 30 можно пользоваться следующей закономерностью:
- критерия при числе наблюдений больше 30 можно пользоваться следующей закономерностью:
если 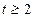 , то критерий достоверен, т.к. соответствует р ≥ 0,95 или р ≤ 0,05;
, то критерий достоверен, т.к. соответствует р ≥ 0,95 или р ≤ 0,05;
если  , то критерий достоверен с большей степенью достоверности, т.к. соответствует р ≥ 0,99 или р ≤ 0,001.
, то критерий достоверен с большей степенью достоверности, т.к. соответствует р ≥ 0,99 или р ≤ 0,001.
Для числа наблюдений меньше 30 достоверность  - критерия определяется по таблице Стьюдента. Для определения табличного значения
- критерия определяется по таблице Стьюдента. Для определения табличного значения  - критерия необходимое число степеней свободы рассчитывается по формуле:
- критерия необходимое число степеней свободы рассчитывается по формуле:  , где
, где  - число наблюдений в одной совокупности;
- число наблюдений в одной совокупности; 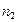 - число наблюдений в другой совокупности.
- число наблюдений в другой совокупности.
Для оценки различий в частотных показателях можно пользоваться таблицей, в которой приводятся минимальные значения разности двух частотных величин, достижения которой достаточно для двукратного превышения своей средней ошибки разности, что подтверждает достоверность различий. Для пользования таблицей достаточно знать меньшее значение из двух показателей и число наблюдений, которое должно быть не меньше 20.
2. При сопоставлении сопряженных совокупностей (двух серий наблюдений на одной и той же совокупности) («до» и «после»)  - критерий рассчитывается разностным методом:
- критерий рассчитывается разностным методом:
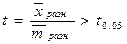 ,
,
где  ,
,  ,
, 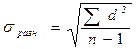 ,
, 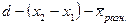
Условные обозначения:
 и
и  - значения показателей в сравниваемых сериях наблюдений (до опыта и после опыта);
- значения показателей в сравниваемых сериях наблюдений (до опыта и после опыта);
 -средняя разность этих показателей;
-средняя разность этих показателей;
 - ошибка репрезентативности разности между показателями;
- ошибка репрезентативности разности между показателями;
 - стандартное отклонение разности между показателями;
- стандартное отклонение разности между показателями;
n - число пар наблюдений.
3. Для сравнения степени однородности статистических групп используется критерий Фишера.
Его значение велико в ряде специальных разделов статистики, особенно в дисперсионном анализе. За  - гипотезу в этом случае принимается признание равенства дисперсий в сравниваемых совокупностях. Критерий Фишера рассчитывается по формуле:
- гипотезу в этом случае принимается признание равенства дисперсий в сравниваемых совокупностях. Критерий Фишера рассчитывается по формуле: 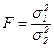 , где
, где 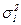 и
и  — дисперсии в сравниваемых совокупностях.
— дисперсии в сравниваемых совокупностях.
Таблица стандартных значений критерия Фишера учитывает объемы сравниваемых групп и выбираемый уровень значимости.

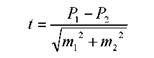
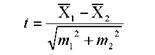
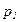 и
и 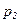 - частотные показатели в сравниваемых совокупностях;
- частотные показатели в сравниваемых совокупностях; 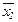 и
и 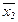 - средние величины в сравниваемых совокупностях;
- средние величины в сравниваемых совокупностях; 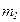 и
и  - ошибки репрезентативности показателей и средних величин в сравниваемых совокупностях.
- ошибки репрезентативности показателей и средних величин в сравниваемых совокупностях. - критерия при числе наблюдений больше 30 можно пользоваться следующей закономерностью:
- критерия при числе наблюдений больше 30 можно пользоваться следующей закономерностью: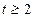 , то критерий достоверен, т.к. соответствует р ≥ 0,95 или р ≤ 0,05;
, то критерий достоверен, т.к. соответствует р ≥ 0,95 или р ≤ 0,05; , то критерий достоверен с большей степенью достоверности, т.к. соответствует р ≥ 0,99 или р ≤ 0,001.
, то критерий достоверен с большей степенью достоверности, т.к. соответствует р ≥ 0,99 или р ≤ 0,001. , где
, где  - число наблюдений в одной совокупности;
- число наблюдений в одной совокупности; 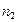 - число наблюдений в другой совокупности.
- число наблюдений в другой совокупности.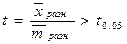 ,
, ,
,  ,
, 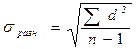 ,
, 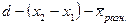
 и
и  - значения показателей в сравниваемых сериях наблюдений (до опыта и после опыта);
- значения показателей в сравниваемых сериях наблюдений (до опыта и после опыта); -средняя разность этих показателей;
-средняя разность этих показателей; - ошибка репрезентативности разности между показателями;
- ошибка репрезентативности разности между показателями; - стандартное отклонение разности между показателями;
- стандартное отклонение разности между показателями; - гипотезу в этом случае принимается признание равенства дисперсий в сравниваемых совокупностях. Критерий Фишера рассчитывается по формуле:
- гипотезу в этом случае принимается признание равенства дисперсий в сравниваемых совокупностях. Критерий Фишера рассчитывается по формуле: 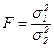 , где
, где 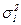 и
и  — дисперсии в сравниваемых совокупностях.
— дисперсии в сравниваемых совокупностях.


