Основные непараметрические методы и условия их применения
40. Значение t - критерия в оценке достоверности различия статистических совокупностей.
Параметрические методы оценки требуют знания характера распределения (только для нормального распределения) изучаемого признака и его параметров (средних величин, стандартного отклонения и др.). Уровень значимости в этих методах определяется с помощью расчета если если
41. Методика расчета t - критерия для двух независимых статистических совокупностей
1. При сопоставлении двух независимых серий наблюдений: для частотных показателей: для средних величин: где Для оценки достоверности полученного если если
42. Особенность оценки t - критерия для больших и малых выборок.
Для числа наблюдений меньше 30 достоверность Для оценки различий в частотных показателях можно пользоваться таблицей, в которой приводятся минимальные значения разности двух частотных величин, достижения которой достаточно для двукратного превышения своей средней ошибки разности, что подтверждает достоверность различий. Для пользования таблицей достаточно знать меньшее значение из двух показателей и число наблюдений, которое должно быть не меньше 20.
43. Область применения, суть методики расчета и оценки метода χ2.
Оценка достоверности различий по методу «хи-квадрат» (критерию соответствия, критерию Пирсона, коэффициенту согласия) Область применения метода: • определение достоверности различий в нескольких сравниваемых группах и при нескольких результатах с определенной степенью достоверности; • определение наличия связи между явлениями без измерения ее величины; • оценка идентичности (близости) распределений двух и более вариационных рядов. Преимущества метода: • не зависит от формы распределения; • может использоваться для сравнения нескольких групп (признаков) • используется на абсолютных цифрах; Ограничения метода: • величина полученного "хи -квадрата" зависит от перегруппировки материала. Если группировки не ярко выражены, результат не показателен; • действует лишь как суммарный показатель различия, не устанавливая отклонение каких именно групп друг от друга обусловило конечный результат, • группы должны быть как можно более однородны для предупреждения "погашения влияний"; • "ожидаемые числа" при расчете должны быть не менее 5; • не следует применять, если число наблюдений < 20 • служит для оценки независимых совокупностей. Суть метода заключается в том, что в сравниваемых группах предполагается отсутствие различий в распределении совокупностей (отсутствие связи между исследуемыми факторами), т.е. формулируется Чем больше теоретические числа, рассчитанные на основе
При альтернативном распределении применяется упрощенная формула, которая рассчитывается на основе таблицы взаимной сопряженности (четырехпольной таблицы):
44. Область применения, суть методики расчета и оценки критерия Вилкоксона.
|


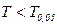
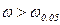
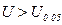
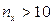 и
и 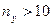
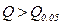
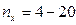 и
и 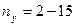
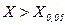
 и
и 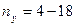
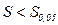
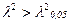
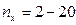 и
и 
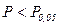
 - критерия и сравнения его значения с табличным, который соответствует определенному уровню значимости:
- критерия и сравнения его значения с табличным, который соответствует определенному уровню значимости: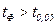 , то
, то 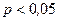 и
и  - гипотеза отвергается;
- гипотеза отвергается;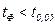 , то
, то 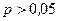 и
и 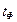 - фактический критерий, рассчитанный в исследовании;
- фактический критерий, рассчитанный в исследовании; 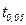 - табличное значение критерия
- табличное значение критерия 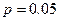 .
.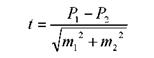

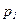 и
и 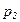 - частотные показатели в сравниваемых совокупностях;
- частотные показатели в сравниваемых совокупностях;  и
и 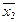 - средние величины в сравниваемых совокупностях;
- средние величины в сравниваемых совокупностях; 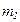 и
и  - ошибки репрезентативности показателей и средних величин в сравниваемых совокупностях.
- ошибки репрезентативности показателей и средних величин в сравниваемых совокупностях.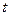 - критерия при числе наблюдений больше 30 можно пользоваться следующей закономерностью:
- критерия при числе наблюдений больше 30 можно пользоваться следующей закономерностью: , то критерий достоверен, т.к. соответствует р ≥ 0,95 или р ≤ 0,05;
, то критерий достоверен, т.к. соответствует р ≥ 0,95 или р ≤ 0,05;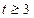 , то критерий достоверен с большей степенью достоверности, т.к. соответствует р ≥ 0,99 или р ≤ 0,001.
, то критерий достоверен с большей степенью достоверности, т.к. соответствует р ≥ 0,99 или р ≤ 0,001.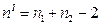 , где
, где 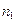 - число наблюдений в одной совокупности;
- число наблюдений в одной совокупности; 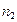 - число наблюдений в другой совокупности.
- число наблюдений в другой совокупности.
 - наблюдаемая частота признака в i - ой группе;
- наблюдаемая частота признака в i - ой группе; 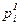 - теоретическая частота, рассчитанная на основе
- теоретическая частота, рассчитанная на основе 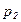

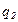
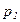



 -альтернативный
-альтернативный 


