Способи задання руху точки
Знати закони руху тіла означає знати закони руху кожної його точки,тому вивчення кінематики почнемо з вивчення руху матеріальної точки. /Траєкторією точки тіла-називають множину (геометричне місце) положень рухомої точки в розглядуваній системі відліку. Залежно від форми траєкторії рух тіла поділяють на п р я м о л і н і й- н и й і криволінійний, Розглянемо два способи задання руху точки: звичайний і координатний. З в и- ч а й н и й спосіб полягає у тому, що рух точки задають її траєкторією і рівнянням руху по цій траєкторії, (законом руху). Рівняння руху с загальному випадку записують так: S = f(t),
де $--відстань точки від початкового положення, що є функцією часу; t — час руху точки від початкового моменту. Знаючи траєкторію точки і рівняння руху по цій траєкторії, можна визначити положення точки у будь-який момент часу: для цього в рівняння S = f(t),треба підставити час. Рухаючись, точка проходить якийсь шлях, то також є функцією часу. Підкреслимо, що шлях, пройде- ний точкою, збігається а відстанню від початку відліку тільки тоді коли точка весь час рухається в одному напрямі і початок її руху збігається з початком відліку: К о о р д и н а т н и й спосіб полягає у тому, що рух точки задають рухом її проекцій вздовж осей координат. Рівняння плоского руху точки y координатному вигляді записують так: x = f(t), y = f1(t).
Знаючи рівняння руху точки, записані у координатному
способом задання руху точки визначити рівняння траєкторії у = f(t), з рівнянь руху треба виключити час. За Міжнародною системою одиниць (СІ) за одиницю довжини беруть метр, а за одиницю часу — секунду.
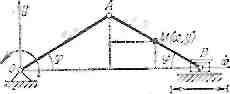
Приклад 9.1. Кривошип ОA обертається навколо нерухомої осі так, що кут φ = 10t рад. Довжина О А = АB = 0,8 м. Знайти рівняння руху і траєкторію середньої точки M шатуна, a також рівняння руху повзуна В, якщо у початковий момент повзун був у крайньому положенні; осі координат показано на рис. 9.3. Р о з в'я з а н н я. Визначимо координати точки М залежно від кута φ: xM = OA*cosφ + AM*cosφ = 0.8*cosφ + 0.4*cosφ = 1.2*cosφ,
yM = MB*sinφ = 0.4*sinφ.
Отже, рівняння руху точки М можна запи- у
хM = І,2*соsІ0t уM = 0,4* sіn 10t. Рис. 9.3 Рис 9.4 Щоб визначити рівняння траєкторії точки М, виключимо з рівняні, руху час. Перетворимо рівняння руху і піднесемо їх до квадрата:
x²M/(1.2)² = cos²10t, y²M/(0.4)² = sin²10t.
Додавши праві і ліні частини цих рівностей. дістанемо рівняння траєкторії точки М: x²M/(1.2)² + y²M/(0.4)² = 1.
Точка М рухається по еліпсу з півосями, що мають довжину 1,2 і 1,4 м. Оскільки повзун В рухається прямолінійно вздовж осі х, то yB = 0.
Щоб скласти рівняння руху повзуна, визначимо абсцису точки В залежно від кута φ: хB = ОA соs φ + AВ соsφ = 0,8 соs φ + 0,8 соs ф = 1,6 cos φ.
Тоді рівняння руху повзуна запишеться:
xB = 1.6*cos10t,м.
Приклад 9.2. Кривошип ОМ куліси Вольфа рівномірно обертається навколо нерухомої осі О так, що кут φ = (π/4)*t рад (рис. 9.4). Довжина стержня ОМ = 0,2 м. У початковий момент стержень ОМ утворював з віссю Ох кут φ0 = 0. Скласти рівняння руху куліси. Р о з в* я з а н н я. З конструкції механізму видно, що куліса рухається зворотнопоступально вздовж осі х. Очевидно, що куліса рухатиметься за таким самим законом,за яким рухається проекція точки М на вісь х, отже, х = xM = OM*cosφ = 0.2*cos(π/4)*t,м.
|

 вигляді, і ставляючи в ці рівняння час, можна знайти проекції точки,
вигляді, і ставляючи в ці рівняння час, можна знайти проекції точки,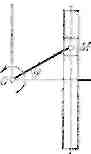 сати так:
сати так: