Указания к лабораторной работе №7
В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя корреляционный анализ, а другая - регрессионный анализ. При оценке тесноты связи между количественными признаками применяется л инейный коэффициент корреляции, который характеризует тесноту и направление связи между двумя признаками в случае наличия между ними линейной зависимости. Данный коэффициент может быть рассчитан по формуле:
Линейный коэффициент корреляции изменяется в пределах от -1 до 1. Если значение коэффициента находится в пределах от 0 до 1, то это свидетельствует о наличии прямой связи между признаками, если в пределах от -1 до 0, то – об обратной связи. При Парная линейная регрессия характеризует линейную связь между признаками: результативным и факторным. Аналитически связь между ними описывается уравнением: Оценка параметров линейного уравнения регрессии Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:
где n - объем исследуемой совокупности (число единиц наблюдения).
В уравнении регрессии параметр Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции При выполнении заданий лабораторной работы №7 необходимо изучить материал, изложенный в [13, стр. 253-260, стр. 271-297 и др.].
|

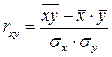 .
.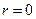 связь между признаками отсутствует, если
связь между признаками отсутствует, если 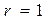 (или
(или 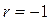 ), то связь является функциональной.
), то связь является функциональной. .
.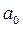 ,
,  осуществляется методом наименьших квадратов (МНК), при котором минимизируется сумма квадратов отклонений фактических значений результативного признака от теоретических.
осуществляется методом наименьших квадратов (МНК), при котором минимизируется сумма квадратов отклонений фактических значений результативного признака от теоретических. ,
, показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; параметр
показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; параметр  - коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения.
- коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения.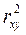 , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю результативного признака, объясняемую регрессией. Чем больше коэффициент детерминации, тем лучше линейная модель регрессии аппроксимирует исходные данные и ею можно пользоваться для прогноза значений результативного признака.
, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю результативного признака, объясняемую регрессией. Чем больше коэффициент детерминации, тем лучше линейная модель регрессии аппроксимирует исходные данные и ею можно пользоваться для прогноза значений результативного признака.


