В в е д е н и е. Количество теплоты, необходимое для нагревания тела на один градус, называют теплоемкостью тела
с = Формула (1) представлена в дифференциальной форме потому, что удельная теплоемкость реальных тел и газов зависит от температуры. Поскольку количество теплоты зависит от процесса, то и теплоемкость существенно зависит от процесса. Молярная теплоемкость вещества – теплоемкость одного моля этого вещества: С = c = где m - молярная масса. Рассмотрим теорию теплоемкости идеального газа. Количество теплоты dQ, переданное системе, затрачивается на увеличение ее внутренней энергии dU и на работу dА, совершаемую системой против внешних сил: dQ = dU + dA = dU + PdV. (4) Если нагревание газа происходит при постоянном объеме, то газ не совершает работы (PdV = 0) и, следовательно, согласно первому началу термодинамики, все количество теплоты идет на увеличение внутренней энергии газа: dQ = dU. (5) Внутренняя энергия одного моля идеального газа U = где i – число степеней свободы молекулы газа, R – универсальная газовая постоянная. Теплоемкость одного киломоля идеального газа при постоянном объеме CV = Если нагревание газа происходит при постоянном давлении, то газ, расширяясь, совершает положительную работу против внешних сил. В соответствии с первым началом термодинамики (4) при изобарическом процессе подведенное количество теплоты расходуется на изменение внутренней энергии газа (dU) и совершение работы (dA), связанное с расширением газа: dQ = dU + PdV. (8) Из уравнения Клапейрона PV = RT (9) следует PdV = RdT (10) и dQ = dU + RdT. (11) CP = где CV = CP = CV + R. (13) Это - уравнение Майера, связывающее теплоемкости изобарного и изохорного процессов: молярная теплоемкость идеального газа при постоянном давлении больше молярной теплоемкости при постоянном объеме на величину универсальной газовой постоянной R. В классической теории теплоемкость идеального газа определяется числом степеней свободы молекул и не зависит от температуры. Для одноатомного газа (i = 3) CV = Если процесс перехода системы из одного состояния в другое протекает без теплообмена с окружающей средой, то такой процесс называется адиабатическим. При таком процессе уравнение (4) примет вид dU + dA = 0 или dA = -dU, (14) т.е. при адиабатическом расширении или сжатии работа совершается газом только за счет изменения запаса внутренней энергии. Уравнение адиабатического процесса (уравнение Пуассона) может быть выведено следующим образом. Поскольку dA = PdV, a dU = CVdT, то уравнение (14) принимает вид: PdV = - CV dT. (15) Разделив это уравнение на (9), получим
или
 = =  = =  – 1. – 1.
Если обозначить (g - 1) Интегрируя и потенцируя уравнение (17), находим ln Vg-1 + ln T = const, T×Vg-1 = const. (18) Используя уравнение состояния (9), получим уравнение Пуассона P×Vg = const. (18) Величина g зависит только от числа степеней свободы молекул, из которых состоит газ. Значения удельной теплоемкости некоторых газов приведены в таблице 1. Таблица 1
Р1=Н+h1, (20) где Н - атмосферное давление; h1 - избыток давления воздуха в баллоне над атмосферным Н, измеряемый манометром и равный разности уровней жидкости в манометре. Затем, если открыть кран П, то сжатый воздух быстро выйдет наружу, так как кран имеет довольно большое отверстие. Как только давление в баллоне снизится и станет равным атмосферному (Н) - кран быстро закрывают. Такой процесс расширения можно считать адиабатическим, так как он протекает быстро и потому без теплообмена.
HV1g = P1V2g, (21) где Н и V1 - давление и объем воздуха в конце процесса; P1 и V2 - давление и объем той же массы газа в начале процесса. Начальное и конечное состояния газа наблюдаются при одинаковой температуре. Поэтому на основании закона Бойля-Мариотта получим P1V2 = P2V1. (22) Решив соответственно уравнения (21) и (22), получим
Логарифмируя(23), найдем lg H – lg P1 = g×(lg P2 – lg P1), откуда g = Поскольку на практике давления Н, Р1 и Р2 незначительно отличаются друг от друга, то в последней формуле разности логарифмов можно заменить разностями самих величин: g = Если учесть, что P1 = H + h1, а Р2 = Н + h2, из уравнения (25) получим расчетную формулу для данного опыта: g = Рассмотренный метод определения отношения Сp/Сv может дать значение, близкое к табличному, только для случая малых сжатий и расширений газа в сосуде.
|

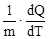 . (1)
. (1) , (2)
, (2)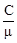 , (3)
, (3)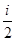 RT, (6)
RT, (6) =
=  =
= 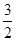 R, CP =
R, CP = 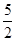 R; для двухатомного (i = 5) CV =
R; для двухатомного (i = 5) CV =  R.
R.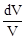 = -
= - 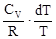
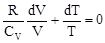 . (16)
. (16)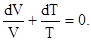 (17)
(17)
 Пусть масса воздуха после накачивания насосом в баллоне объемом V1 равна m. При открывании крана часть воздуха (Dm) выходит. Тогда масса оставшегося воздуха m1 = m - Dm. Масса воздуха m1, которая заключается в объеме V1, занимала перед открытием крана меньший объем V2. Таким образом, уравнение (19) для массы газа m1 в нашем случае, примет вид:
Пусть масса воздуха после накачивания насосом в баллоне объемом V1 равна m. При открывании крана часть воздуха (Dm) выходит. Тогда масса оставшегося воздуха m1 = m - Dm. Масса воздуха m1, которая заключается в объеме V1, занимала перед открытием крана меньший объем V2. Таким образом, уравнение (19) для массы газа m1 в нашем случае, примет вид: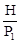 =
=  . (23)
. (23)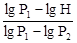 . (24)
. (24) . (25)
. (25)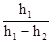 . (26)
. (26)


