Практикум. Линейные и евклидовы пространства
В данном практикуме рассматриваются следующие основные задачи: 1) исследование системы векторов на линейную зависимость и линейную независимость; 2) нахождение базиса и размерности линейного пространства решений однородной системы линейных алгебраических уравнений; 3) построение базиса в линейном пространстве; 4) нахождение формул преобразования координат при переходе от базиса к базису, разложение вектора по векторам базиса; 5) построение ортогонального и ортонормированного базисов методом ортогонализации Грама-Шмидта; 6) дополнение системы векторов до ортогонального базиса в евклидовом пространстве. Примеры задач, рассматриваемых в данном практикуме, соответствуют заданиям 1, 2, 3, 4, 5 типового расчета. Пример 1. Исследовать систему векторов
пространства Решение. Составим линейную комбинацию
из векторов системы
Получим
Пользуясь правилами умножения числа на вектор-столбец и сложения двух вектор-столбцов, упростим левую часть последнего уравнения в (1)
Итак, получили равенство
Два вектор-столбца равны, когда равны соответствующие компоненты. В результате приходим к системе однородных линейных алгебраических уравнений
Основная матрица
Найдем определитель матрицы
Так как определитель
Это означает, что равенство (1) выполняется только при нулевых значениях чисел Эту же задачу можно решить и другим способом. Известно, что система вектор-столбцов Пример 2. Исследовать систему векторов
пространства Решение. Составим линейную комбинацию
из векторов системы Получим
Как и при решении примера 1, пользуясь правилами умножения числа на вектор-столбец и сложения двух вектор-столбцов, упрощая равенство (3), приходим к следующему равенству
В результате получаем систему однородных линейных алгебраических уравнений
Основная матрица
Найдем определитель матрицы
Так как определитель Для этого используем метод Гаусса решения системы (используем элементарные преобразования над строками основной матрицы
Последняя матрица есть ступенчатая матрица. Ранг ее равен 2, система (4) имеет бесконечное множество решений. В качестве базисных (основных) переменных выберем переменные
Выражая базисные переменные
Взяв в качестве
Это означает, что равенство (3) выполняется при ненулевых значениях чисел При найденных значениях
Из последнего равенства удобно выразить вектор
Пример 3. Найти базис и размерность линейного пространства
Решение. Приводим матрицу системы к ступенчатому виду
(во второй матрице три одинаковые строки, значит, последние две из них можно обнулить). Итак, ступенчатая матрица имеет вид
Ранг матрицы
Составляем базис
Пример 4. Дана система векторов
1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
в базисе
|

 :
:
 на линейную зависимость.
на линейную зависимость.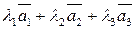
 и приравняем ее к нулевому вектору
и приравняем ее к нулевому вектору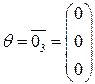 .
. (1)
(1)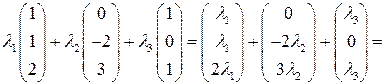


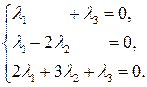 (2)
(2) этой системы имеет вид (элементами матрицы являются коэффициенты при неизвестных
этой системы имеет вид (элементами матрицы являются коэффициенты при неизвестных  .
.
 отличен от нуля, то матрица
отличен от нуля, то матрица 
 , является неособенной матрицей (ее определитель отличен от нуля). Так как в этом случае эта матрица совпадает с матрицей
, является неособенной матрицей (ее определитель отличен от нуля). Так как в этом случае эта матрица совпадает с матрицей 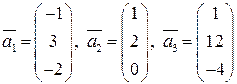
 .
.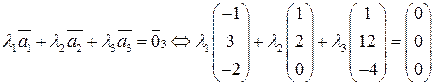 . (3)
. (3)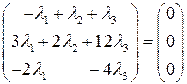 .
. (4)
(4) .
.

 , то матрица
, то матрица 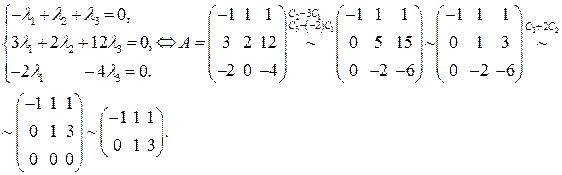
 (при этом
(при этом  является свободной переменной). Переходя от ступенчатой матрицы к системе уравнений, получим
является свободной переменной). Переходя от ступенчатой матрицы к системе уравнений, получим
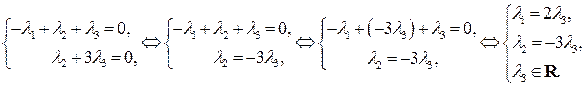

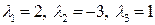 равенство (3) примет вид
равенство (3) примет вид
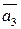 в виде линейной комбинации векторов
в виде линейной комбинации векторов  :
: .
.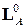 решений однородной системы линейных алгебраических уравнений
решений однородной системы линейных алгебраических уравнений

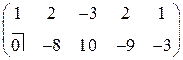 .
. . Принимая переменные
. Принимая переменные  за базисные, а
за базисные, а  за свободные (обозначаем при этом
за свободные (обозначаем при этом 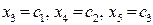 ), получим общее решение рассматриваемой ОСЛАУ
), получим общее решение рассматриваемой ОСЛАУ
 пространства решений
пространства решений  ):
):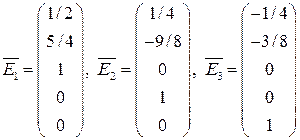 .
.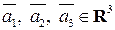 :
: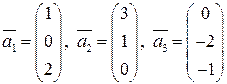 .
. , написать матрицу
, написать матрицу  перехода от стандартного базиса
перехода от стандартного базиса  пространства
пространства 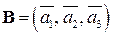 .
.