Решение. 1. Для доказательства того, что система векторов является базисом в пространстве , достаточно найти определитель матрицы
1. Для доказательства того, что система векторов
Так как определитель матрицы отличен от нуля, то система векторов 2. Напишем формулы преобразования координат при переходе от стандартного базиса
к базису Разложим векторы
Аналогично можно поступить и с остальными векторами. В результате получаем следующую систему
Составляем матрицу
перехода от стандартного базиса Теперь составим формулы преобразования координат при переходе от базиса к базису. Пусть вектор
а в базисе
Тогда имеет место формула
где Найдем обратную матрицу
где Для удобства вычислений составим таблицу алгебраических дополнений:
В результате обратная матрица
При этом формула (5) примет вид
Расписывая покоординатно последнее матричное равенство, получим систему, описывающую связь координат вектора в новом базисе
или
Итак, формулы преобразования координат при переходе от базиса
то пользуясь формулами (6), найдем координатный вектор-столбец вектора
Пример 5. Даны векторы
Найти нормы этих векторов в соответствующих евклидовых пространствах, если скалярное произведение в каждом из них задано в стандартном виде
Пронормировать векторы согласно выбранной норме (построить соответствующие единичные векторы
|

 является базисом в пространстве
является базисом в пространстве  , достаточно найти определитель матрицы, составленной из компонент этих векторов:
, достаточно найти определитель матрицы, составленной из компонент этих векторов:
 :
:
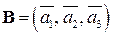 .
.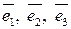 . Например, вектор
. Например, вектор 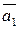 раскладывается следующим образом:
раскладывается следующим образом: .
.

 в базисе
в базисе 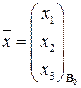 ,
, .
. , (5)
, (5)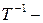 матрица, обратная к матрице
матрица, обратная к матрице  перехода.
перехода.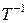 по формуле
по формуле ,
, алгебраическое дополнение для элемента
алгебраическое дополнение для элемента 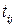 матрицы перехода
матрицы перехода  ).
).






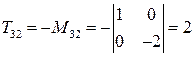


 .
.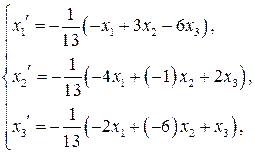
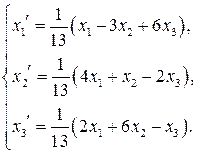 (6)
(6) к базису
к базису  имеют вид (6). Теперь если вектор
имеют вид (6). Теперь если вектор  имеет в базисе
имеет в базисе 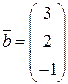 ,
, (подставляем в формулы (6)
(подставляем в формулы (6)  )
)
 .
. .
. ).
).


