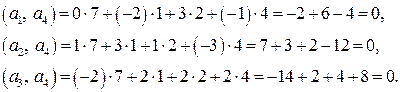Решение. Проведем процесс ортогонализации Грама-Шмидта системы векторов базиса .
Проведем процесс ортогонализации Грама-Шмидта системы векторов 1) На первом шаге необходимо вычислить векторы
затем скалярное произведение и норму вектора
и окончательно вектор
2) На втором шаге необходимо вычислить векторы
затем вектор
Теперь нормируем вектор
получаем вектор
3) На третьем шаге необходимо вычислить векторы
затем вектор
Теперь нормируем вектор
получаем последний искомый вектор
Итак, ортонормированный базис
Пример 7. Проверить ортогональность векторов
Решение. Решение задачипредусматривает нахождение двух векторов Проверим ортогональность векторов
Так как Найдем вектор
Эту однородную систему решим методом Гаусса. Приводим матрицу системы к ступенчатому виду (меняем местами строки матрицы)
Ранг матрицы
Итак, общее решение однородной системы имеет вид
Из множества решений выделим частное решение. Положим (для дальнейшего удобства)
Выполним проверку:
Найдем вектор
Эту однородную систему решим методом Гаусса. Приводим матрицу системы к ступенчатому виду
Ранг ступенчатой матрицы
Из множества решений выделим частное решение. Положим (для дальнейшего удобства)
Выполним проверку:
Ответ: ортогональный базис имеет вид
|

 базиса
базиса  .
. . Вычисляем вектор
. Вычисляем вектор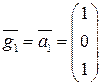 ,
,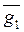
 ,
,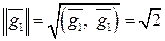 ,
, ,
,  .
. . Сначала вычисляем скалярное произведение
. Сначала вычисляем скалярное произведение ,
,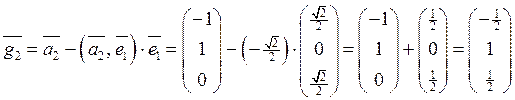 .
. :
: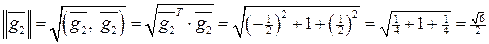 ,
,
 ,
,  .
. . Сначала вычисляем скалярные произведения
. Сначала вычисляем скалярные произведения ,
,  ,
,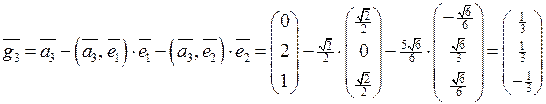 .
. :
: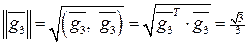 ,
,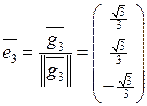 ,
, 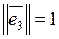 .
. состоит из векторов:
состоит из векторов: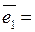
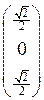 ,
,  ,
,  .
.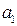 ,
,  пространства
пространства  и дополнить эти векторы до ортогонального базиса:
и дополнить эти векторы до ортогонального базиса: .
.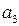 ,
, 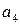 таких, что система векторов
таких, что система векторов 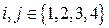 (
( )
)  (любые два разных вектора из системы ортогональны).
(любые два разных вектора из системы ортогональны). этих векторов:
этих векторов: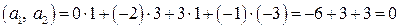 .
. , то векторы
, то векторы 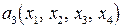 такой, что он ортогонален векторам
такой, что он ортогонален векторам  . В результате приходим к системе уравнений
. В результате приходим к системе уравнений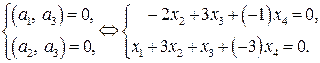
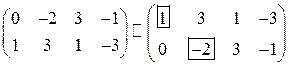 .
. . Принимая переменные
. Принимая переменные  за базисные, а
за базисные, а  за свободные (обозначаем при этом
за свободные (обозначаем при этом  ), получим общее решение рассматриваемой ОСЛАУ
), получим общее решение рассматриваемой ОСЛАУ

 . Тогда получим
. Тогда получим 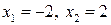 . Итак, вектор
. Итак, вектор 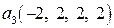 .
.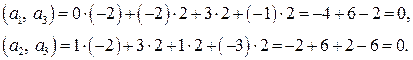
 такой, что он ортогонален векторам
такой, что он ортогонален векторам 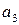 , то есть
, то есть  . В результате приходим к системе уравнений
. В результате приходим к системе уравнений

 . Принимая переменные
. Принимая переменные 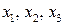 за базисные, а
за базисные, а  - за свободную (обозначаем при этом
- за свободную (обозначаем при этом  ), получим общее решение рассматриваемой ОСЛАУ
), получим общее решение рассматриваемой ОСЛАУ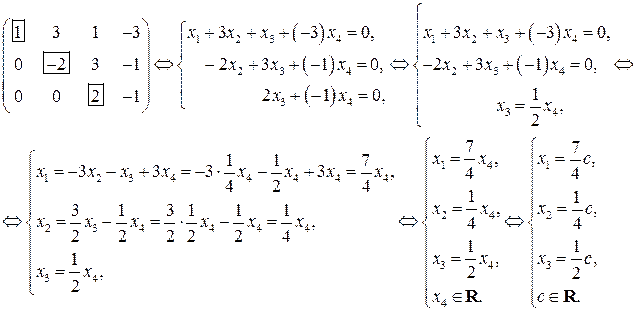
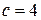 . Тогда получим
. Тогда получим  . Итак, вектор
. Итак, вектор  имеет вид
имеет вид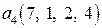 .
.