Центрированные оптические системы (ЦОС).
Оптическая система, образованная сферическими отражающими и преломляющими поверхностями, называется центрированной, если центры кривизны всех поверхностей лежат на одной прямой. Эта прямая называется главной оптической осью системы. Если пучок лучей, исходящих из какой-либо точки S, после прохождения некоторой оптической системы сходится в точке Si , то Si является стигматическим изображением точки S. S и Si называются сопряженными точками. Под идеальной оптической системой понимают такую систему, которая дает стигматическое изображение, геометрически подобное отображенному предмету. Теория таких систем становится особенно простой, когда все распространяющиеся в них лучи параксиальны, т.е. проходят на небольшом расстоянии от оптической оси системы и образуют с ней малые углы.
ЦОС характеризуется рядом так называемых кардинальных точек и плоскостей, задание которых полностью описывает все свойства ЦОС и позволяет пользоваться ими, не рассматривая реального хода лучей в системе.
На рис.3 изображена некоторая ЦОС, ограниченная сферическими поверхностями MM и NN. Направим на эту систему луч A1B1, параллельный главной оптической оси OO1. Сопряженный ему луч выйдет из системы по направлению C2D2 и пересечет главную оптическую ось в точке F2 - заднем главном фокусе ЦОС. Плоскость, проходящая через F2 и перпендикулярная главной оптической оси OO1,называется фокальной. Точно так же луч A2B2 при прохождении через систему пересечет ось OO1 в точке F1 - переднем главном фокусе ЦОС. Лучи, исходящие из точек F1 и F2, после системы будут идти параллельно главной оптической оси.Продолжения лучей A1B1 и D1C1 (A2B2 и D2C2)пересекаются в точке R1 (R2). Плоскости, проходящие через точки R1 и R2 и перпендикулярные оптической оси, носят названия главныхплоскостей, а точки H1 и H2 - главных точек. Точки главных плоскостей R1 и R2 сопряжены и изображаются с линейным увеличением +1. Точки H1, H2, F1 и F2 являются кардинальными точками ЦОС. Расстояния от главных точек до фокусов f1=H1F1 и f2=H2F2 называются фокусными расстояниями системы. Главный фокус может лежать как слева, так и справа от соответствующей главной точки. Чтобы отличать эти два случая необходимо пользоваться правилом знаков: если отсчет отрезков производится от главных точек к фокусу против хода луча, то фокусное расстояние равно длине отрезка, умноженного на –1, если по ходу луча, то на +1. В соответствии с этим на рис.3 фокусное расстояние f1 отрицательная величина, а f2 – положительная. Обратим внимание, что на рисунках указываются длины отрезков, то есть модули соответствующих величин (например, - f1, f2, рис.3). Число кардинальных точек в общем случае равно четырем. В некоторых частных случаях их число уменьшается, например, в тонкой линзе обе главные плоскости сливаются в одну. У телескопической системы кардинальные точки находятся на бесконечности, и поэтому построение изображения с их помощью невозможно. В качестве кардинальных точек не обязательно пользоваться фокусами и главными точками, иногда их заменяют узловыми точками. Они обладают тем свойством, что луч, проходящий через переднюю узловую точку (К1, рис.4) и образующий с осью ОО¢ угол a, после преломления проходит через заднюю узловую точку (К2) и образует с осью тот же угол a (в сопряженных точках К1 и К2 угловое увеличение равно +1). Если значения показателей преломления первой и последней сред одинаковы, то узловые точки совпадают с главными.
Вообще говоря, в качестве кардинальных точек можно принять две произвольно выбранные пары сопряженных точек при условии, что известно линейное или угловое увеличение, соответствующее этим парам. Однако применение таких кардинальных точек неудобно и не получило распространение на практике. Рис.5 дает представление о том, как геометрическим построением найти изображение предмета, используя кардинальные элементы ЦОС.
Простейшей оптической системой является линза, которая состоит из двух преломляющих поверхностей, разделенных оптически однородным промежутком.
Если толщина этого промежутка мала по сравнению с радиусами кривизны преломляющих поверхностей, то линза называется тонкой. Главные и узловые плоскости тонкой линзы совпадают друг с другом. Пересечение этой плоскости с оптической осью называется оптическим центром линзы О (рис.6). Если среды по обе стороны тонкой линзы одинаковы, то луч, проходящий через точку О, не преломляется, а f2 = - f1. Положение объекта и изображения в тонкой линзе определяются расстояниями a1 и a2, отсчитанными от оптического центра линзы. Они связаны между собой соотношением:
Величины, входящие в это уравнение, являются алгебраическими. В соответствии с правилом знаков, если отсчет отрезков производится от центра линзы против хода луча, то длина отрезка умножается на –1, если по ходу луча - то на +1.
|

 Рис.3. Кардинальные точки и плоскости центрированной оптической системы.
Рис.3. Кардинальные точки и плоскости центрированной оптической системы.
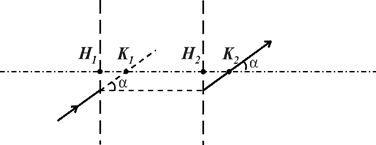 Рис.4. Узловые точки К1 и К2 центрированной оптической системы.
Рис.4. Узловые точки К1 и К2 центрированной оптической системы.
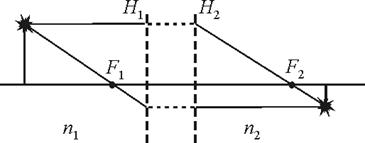 Рис.5. Ход лучей в центрированной оптической системе.
Рис.5. Ход лучей в центрированной оптической системе.
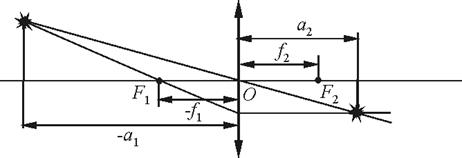 Рис.6. Ход лучей в тонкой линзе
Рис.6. Ход лучей в тонкой линзе
 . (2)
. (2)


