Dispose(q)

End

end; { Delete1 }

Результат применения алгоритма Delete1 к дереву, изображенному на рисунке 6 а), выглядит так, как показано на рисунке 6 в). Можно заметить, что при использовании этого алгоритма дерево подвергается большей деформации, чем при применении алгоритма Delete (см. рисунок 6 б)).

Процедура Insert, используемая в Delete1, является универсальной и для данного случая включения может быть упрощена, так как известно, что правое поддерево должно быть подсоединено к самой правой пустой ссылке. В этом случае можно выполнить нерекурсивную реализацию процедуры включения в дерево поиска:

procedure Insert1(T: Tree; p: Tree);

var s: Tree;

Begin

s:=T; {по условию использования T<>nil}

while s^.R <> nil do

s:=s^.R;

s^.R:=p;

end; { Insert1 }

Упражнение 4.6. Описать процедуру исключения слова из частотного словаря (см. раздел 4.2 и пример 4.3).

 

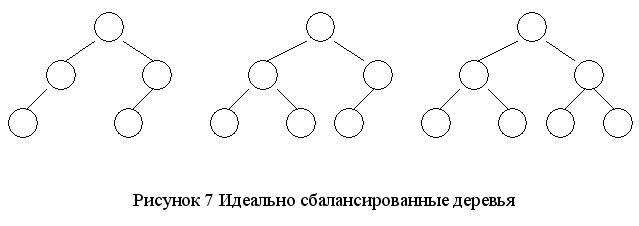
5. СБАЛАНСИРОВАННЫЕ ДЕРЕВЬЯ

 

Дерево называется идеально сбалансированным, если число вершин
(узлов) в его левых и правых поддеревьях отличается не более чем на единицу (рисунок 7).

Алгоритм построения идеально сбалансированного дерева основан на следующих правилах:

Создаем узел дерева.

Строим тем же способом левое поддерево.

Строим тем же способом правое поддерево.

Способ построения определяется поставленной задачей. Процесс построения заканчивается, если исчерпаны данные.

Пример 5.1. Построить дерево минимальной глубины, состоящее из n вершин (на рисунке 7 n = 5,6,7).

Минимальная глубина при заданном числе вершин достигается, если на всех уровнях, кроме последнего, помещается тоже максимально возможное число вершин.

Рекурсивная функция Balance строит идеально сбалансированного дерево с n вершинами, значения которых читаются из файла F:

function Balance(n: integer): Tree;

var p: Tree;

nl,nr: integer;

Begin

if n=0 then p:=nil

Else

Begin