new(p);

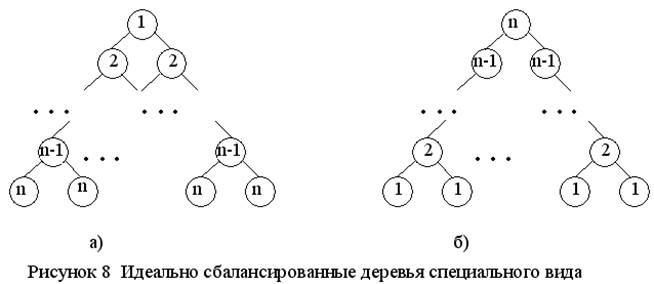
with p^ do

Begin

Read(F,inf);

nl:=n div 2; nr:=n-nl-1;

L:=Balance(nl); R:=Balance(nr);

End

End;

Balance:=P

end; { Balance }

Пример 5.2. Построить идеально сбалансированное дерево, изображенное на рисунке 8 а).

Число уровней дерева на рисунке 8 а) – n. Значение k вершины на каждом уровне дерева меняется от 1 до n.

Рекурсивная функция Tree_1n построения дерева T вида 8 а) имеет 3 параметра (T, n, k) и может быть описана так:

procedure Tree_1n(var T: Tree; n,k: integer);

var i: integer;

Begin

if k > n then T:=nil

Else

Begin

new(T); T^.inf:=k;

Tree_1n (T^.L, n, k+1);

Tree_1n (T^.R, n, k+1);

End

end; { Tree_1n }

Обращение к процедуре Tree_1n для построения дерева Root заданным способом будет иметь вид: Tree_1n(Root,n,1);

Процедуры включения и исключения, восстанавливающие идеально сбалансированное дерево, – довольно сложные операции и не всегда оправданы. Менее строгое определение сбалансированного дерева было предложено
Г.М. Адельсоном-Вельским и Е.М. Ландисом:

Дерево называется сбалансированным тогда и только тогда, когда
высоты двух поддеревьев каждой из его вершин отличаются не более чем на единицу.

Деревья, удовлетворяющие такому условию, называют равновесными [7] или АВЛ – деревьями. Идеально сбалансированные деревья являются частным случаем АВЛ – деревьев.

Процедуры включения и исключения, сохраняющие сбалансированностьдеревьев, подробно описаны в [ 2, 4 ].

Упражнение 5.1. Описать процедуру построения дерева, изображенного на рисунке 8 а), используя два параметра (T, n).

Упражнение 5.2. Описать процедуру построения дерева, изображенного на рисунке 8 б).

ЛИТЕРАТУРА

 

1 Абрамов В.Г., Трифонов Н.П., Трифонова Г.Н. Введение в язык
паскаль. – М.: Наука,1988.–320 с.

2 Вирт Н. Алгоритмы и структуры данных. – М.: Мир, 1989. –360 с.

3 Вьюкова Н.И., Галатенко В.А., Ходулев А.Б. Систематический подход к программированию. - М.: Наука, 1988.– 208 с.

4 Кнут Д. Искусство программирования для ЭВМ. Том 1. Основные
алгоритмы. - М.: Мир, 1976. – 736 с.

5 Кнут Д. Искусство программирования для ЭВМ. Том 3. Сортировка и поиск. - М.: Мир, 1978. – 844 с.

6 Мейер Б., Бодуэн К. Методы программирования: В 2-х томах. Т.1. -М.: Мир, 1982. – 356 с.

7 Мейер Б., Бодуэн К. Методы программирования: В 2-х томах. Т.2. -М.: Мир, 1982. – 368 с.

8 Методы программирования. Учебное пособие / Минакова Н.И.,
Невская Е.С., Угольницкий Г.А., Чекулаева А.А., Чердынцева М.И. – М.:
Вузовская книга, 1999. – 280 с.

9 Пильщиков В.Н. Сборник упражнений по языку Паскаль. – М.: Наука, 1989. – 160 с.

10. Амелина Н.И., Русанова Я.М., Пасечный Л.Г. Языки программирования и методы трансляции. Задания по учебной практике. Методические указания для студентов 2 курса вечернего отделения механико-математического
факультета. – Ростов-на-Дону, УПЛ РГУ, 2006. – 16 с.