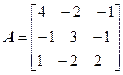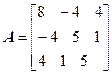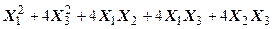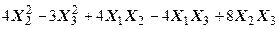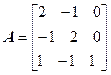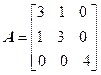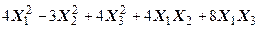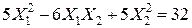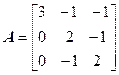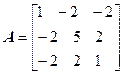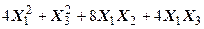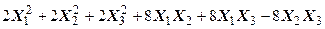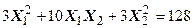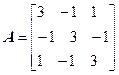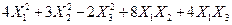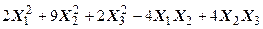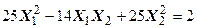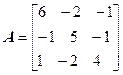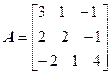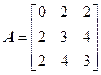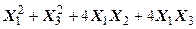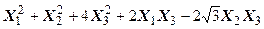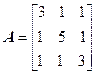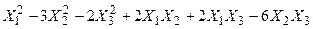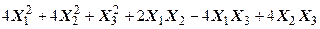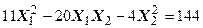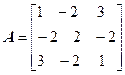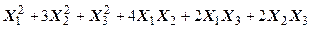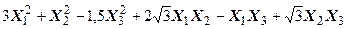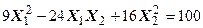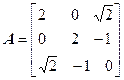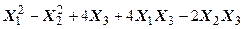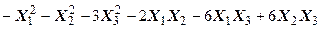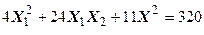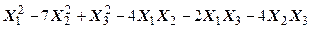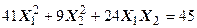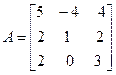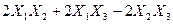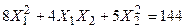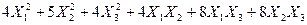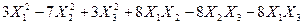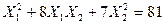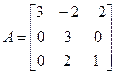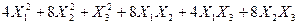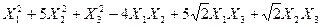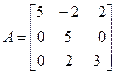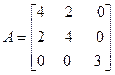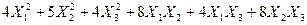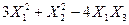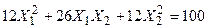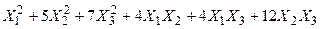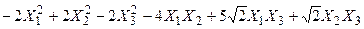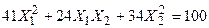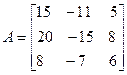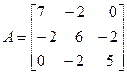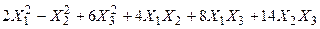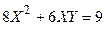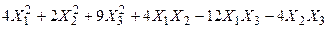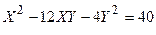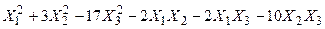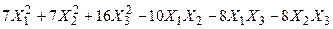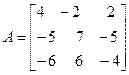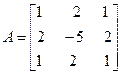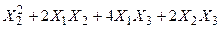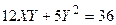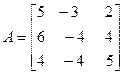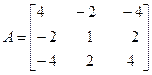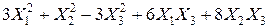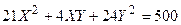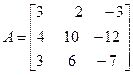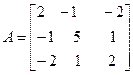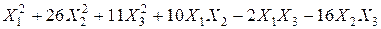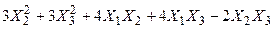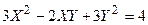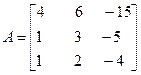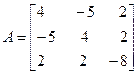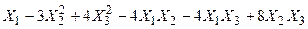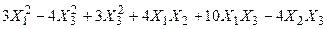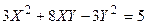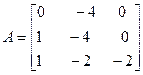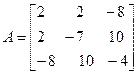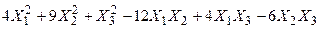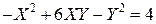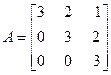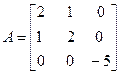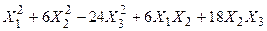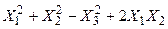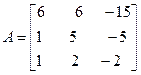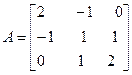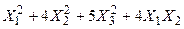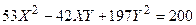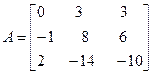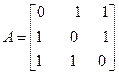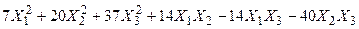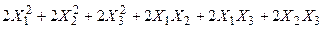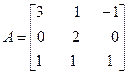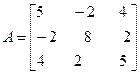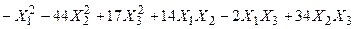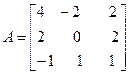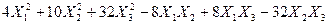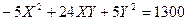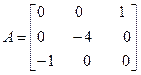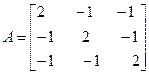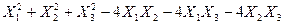ЛИНЕЙНЫЕ И ЭВКЛИДОВЫ ПРОСТРАНСТВА». Задача №4.Найти собственные значения и собственные векторы линейного оператора, заданного в некотором базисе матрицей А.

ЛИНЕЙНАЯ АЛГЕБРА. ТР №1.ЧАСТЬ 2.

Задача №4. Найти собственные значения и собственные векторы линейного оператора, заданного в некотором базисе матрицей А.

Задача №5. Привести матрицу А к диагональному виду, указать собственную матрицу перехода.

Задача №6. Привести квадратичную форму к каноническому виду методом Лагранжа.

Задача № 7. Привести квадратичную форму к каноническому виду ортогональным преобразованием.

Задача № 8. Найти канонический вид заданной квадратичной формы и построить на плоскости 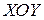линию, определяемую заданным уравнением.

№ зад.	Вариант 1.







№ зад.	Вариант 2.







№ зад.	Вариант 3.







№ зад.	Вариант 4.







№ зад.	Вариант 5.







№ зад.	Вариант 6.







№ зад.	Вариант 7.







№ зад.	Вариант 8.







№ зад.	Вариант 9.







№ зад.	Вариант 10.







№ зад.	Вариант 11.







№ зад.	Вариант 12.







№ зад.	Вариант 13.







№ зад.	Вариант 14.







№ зад.	Вариант 15.







№ зад.	Вариант 16.







№ зад.	Вариант 17.







№ зад.	Вариант 18.







№ зад.	Вариант 19.







№ зад.	Вариант 20.







№ зад.	Вариант 21.







№ зад.	Вариант 22.







№ зад.	Вариант 23.







№ зад.	Вариант 24.







№ зад.	Вариант 25.







№ зад.	Вариант 26.







№ зад.	Вариант 27.







№ зад.	Вариант 28.






№ зад.	Вариант 29.







№ зад.	Вариант 30.

<== предыдущая лекция	\|	следующая лекция ==>
ЛИНЕЙНЫЕ И ЭВКЛИДОВЫ ПРОСТРАНСТВА».	\|	Функции участников деловой игры

Дата добавления: 2015-08-12; просмотров: 381. Нарушение авторских прав; Мы поможем в написании вашей работы!

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...

Различия в философии античности, средневековья и Возрождения ♦Венцом античной философии было: Единое Благо, Мировой Ум, Мировая Душа, Космос...

Характерные черты немецкой классической философии 1. Особое понимание роли философии в истории человечества, в развитии мировой культуры. Классические немецкие философы полагали, что философия призвана быть критической совестью культуры, «душой» культуры. 2. Исследовались не только человеческая...

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит...

ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ Сила, с которой тело притягивается к Земле, называется силой тяжести...

СПИД: морально-этические проблемы Среди тысяч заболеваний совершенно особое, даже исключительное, место занимает ВИЧ-инфекция...

Понятие массовых мероприятий, их виды Под массовыми мероприятиями следует понимать совокупность действий или явлений социальной жизни с участием большого количества граждан...

Studopedia.info - Студопедия - 2014-2026 год . (0.01 сек.) русская версия | украинская версия