Портфель из двух активов.
Формулы расчета для расчета доходности и риска портфеля значительно упрощаются и становятся наглядными, если портфель составлен из двух бумаг. Пример 1. Для портфеля из двух акций А и В рассчитать ожидаемую доходность портфеля, стандарное отклонение для различных значений долей акций в портфеле. Построить эффективное множество. Каким значениям корреляции соответствуют границы портфеля.
Риск и доходность портфеля из двух бумаг легко находится из формул
(8) Поскольку сумма весов в портфеле должна быть равна единице, то выразим вес акции 2 через вес акции 1 - w1 w2 = 1 - w1 (9) Подставляя теперь (9) в выражения для доходности и риска портфеля (8) получим
Если для различных значений корреляции между бумагами А и Б и долями бумаг в портфеле построить множество Рис.2 Границы множества Марковица для различных значений коэффициента корреляции активов, входящих в портфель
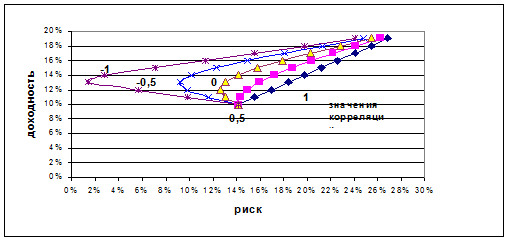
Граница имеет вид пули. Это легко можно объяснить, если рассмотреть случай двух типов акций позицией. При запрещенной короткой позиции вес каждой бумаги в портфеле должен быть неотрицательным. Риск можно полностью исключить, если бумаги имеют отрицательную корреляцию. Стратегия Марковица заключается в том, что с ростом корреляции доходностей активов, входящих в портфель увеличивается вариация портфеля и включение в портфель активов с отрицательной корреляцией уменьшает риск портфеля. На практике таких активов очень мало Границу множества портфелей Марковица называют эффективной границей Марковица. Портфели, лежащие вне этой границы недостижимы, а внутри неэффективны. Пусть теперь необходимо найти портфель с минимальным риском. Это означает, что первая производная по дисперсии должна быть равна нулю.
Решая относительно
Минимальный риск будет при корреляции равной Пример. Дисперсии (вариаци) равны
Подставляя (13) в выражении для среднеквадратического отклонения (10) найдем риск портфеля из двух бумаг
|


 (10)
(10) , то получим множество возможных портфелей, которое получило название множество Марковица. Для коэффициентов корреляций {-1;-0,5;0;0,5;1} по формулам были найдены соответствующие значения доходности r p и риска σp портфеля. Результаты расчетов показаны на рис.2
, то получим множество возможных портфелей, которое получило название множество Марковица. Для коэффициентов корреляций {-1;-0,5;0;0,5;1} по формулам были найдены соответствующие значения доходности r p и риска σp портфеля. Результаты расчетов показаны на рис.2
 (11)
(11) получим долю акций типа А в портфеле
получим долю акций типа А в портфеле (12)
(12) , а максимальный при корреляции равной единице
, а максимальный при корреляции равной единице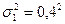 ,
, 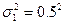 ,
,  . Минимальный риск будет иметь портфель, содержащий долю акций типа А равную
. Минимальный риск будет иметь портфель, содержащий долю акций типа А равную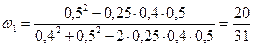 (13)
(13) 3,48%
3,48%


