Доходность облигации
Доходность облигации характеризуется рядом параметров, которые зависят от условий, предложенных эмитентом. Так, например, для облигаций, погашаемых в конце срока, на который они выпущены, доходность измеряется: купонной доходностью; текущей доходностью; полной доходностью. Купонная доходность Купонная доходность — норма процента, которая указана на ценной бумаге и которую эмитент обязуется уплатить по каждому купону. Платежи по купонам могут производиться раз в квартал, по полугодиям или раз в год. Например, на облигации указана купонная доходность в 11,75% годовых. Номинал облигации — 1,0 тыс. руб. На каждый год имеется два купона. Это значит, что облигация принесет полугодовую прибыль 58,75 руб. (1,0 • 0,1175 • 0,50), а за год — 117,5 руб. Текущая доходность Текущая доходность (CY) облигации с фиксированной ставкой купона — определяется как отношение периодического платежа к цене приобретения. Текущая доходность характеризует выплачиваемый годовой процент на вложенный капитал, т.е. на сумму, уплаченную в момент приобретения облигации. Текущая доходность определяется по формуле:
Например, если купонная доходность — 11,75%, а курс облигации — 95,0, то ее текущая доходность составит:
Вместе с тем текущая доходность не учитывает изменения цены облигации за время ее хранения, т.е. другого источника дохода. Текущая доходность продаваемых облигаций меняется в соответствии с изменениями их цен на рынке. Однако с момента покупки она становится постоянной (зафиксированной) величиной, так как ставка купона остается неизменной. Нетрудно заметить, что текущая доходность облигации, приобретенной с дисконтом, будет выше купонной, а приобретенной с премией — ниже. Показатель текущей доходности не учитывает курсовую разницу между ценой покупки и погашения. Поэтому он не пригоден для сравнения эффективности операций с различными исходными условиями. В качестве меры общей эффективности инвестиций в облигации используется показатель доходности к погашению. Доходность к погашению Доходность к погашению (YTM) — это процентная ставка в коэффициенте дисконтирования, которая устанавливает равенство между текущей стоимостью потока платежей по облигации и её рыночной ценой.
Рассмотрим некоторые важнейшие свойства этого показателя. По сути он представляет собой внутреннюю доходность инвестиции (IRR). Однако, реальная доходность облигации к погашению будет равна YTM только при выполнении следующих условий: облигация хранится до срока погашения; полученные купонные доходы немедленно реинвестируются по ставке Очевидно, что независимо от желаний инвестора второе условие достаточно трудно выполнить на практике. Между доходностью к погашению и ставкой реинвестирования купонного дохода существует прямая зависимость. С уменьшением будет уменьшаться и величина, с ростом величина будет также расти. Полная доходность Полная доходность учитывает все источники дохода. В ряде экономических публикаций показатель полной доходности называют ставкой помещения. Определив ставку помещения в виде годовой ставки сложных или простых процентов, можно судить об эффективности приобретенной ценной бумаги. Начисление процентов по ставке помещения на цену приобретения дает доход, эквивалентный фактически получаемому по ней доходу за весь период обращения этой облигации до момента ее погашения. Ставка помещения является расчетной величиной и в явном виде на рынке ценных бумаг не выступает. При определении доходности облигации учитывается цена приобретения (рыночная цена), которая сама зависит от ряда факторов. Покупатель облигации в момент ее приобретения рассчитывает на получение дохода в виде серии твердых выплат в форме фиксированных процентов, которые осуществляются в течение всего срока ее обращения, а также возмещение ее номинальной стоимости к концу этого срока. Поэтому если ежегодно получаемые по облигациям выплаты будут помещены на банковский депозит или инвестированы каким-либо иным образом и станут приносить ежегодный процентный доход то стоимость облигации будет равна сумме двух слагаемых — современной стоимости ее аннуитетов (серии ежегодных выплат процентных платежей) и современной стоимости ее номинала:
или
В случае когда облигация предусматривает выплату процентов по полугодиям или поквартально, курсовая стоимость облигации рассчитывается по формулам:
Пример. По облигации номинальной стоимостью 10,0 тыс. руб. в течение 10 лет (срок до ее погашения) будут выплачиваться ежегодно в конце года процентные платежи в сумме 1,0 тыс. руб. (g= 10%), которые могут быть помешены в банк под 11% годовых. Определим цену облигации при разных процентных ставках. Рыночная цена облигации по формуле (9.3) составит:
а рыночный курс:
|


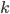 — норма доходности по купонам (годовая ставка купона);
— норма доходности по купонам (годовая ставка купона); 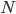 — номинальная цена облигации;
— номинальная цена облигации;  — рыночная цена (цена приобретения);
— рыночная цена (цена приобретения);  — курс в момент приобретения.
— курс в момент приобретения. 

 .
. (9.3)
(9.3)
 — купонная ставка;
— купонная ставка;  — время от момента приобретения до момента погашения облигации;
— время от момента приобретения до момента погашения облигации;  — ссудный процент, предлагаемый банками в момент продажи облигации.
— ссудный процент, предлагаемый банками в момент продажи облигации. 





