Основные показатели корреляционно-регрессионного анализа
При изучении тесноты связи между двумя взаимозависимыми рядами применяется линейный коэффициент корреляции, который показывает, существует ли и насколько велика связь между этими рядами. Он может принимать значения в пределах от – 1 до +1. Если линейный коэффициент корреляции отрицателен, то это говорит об обратной связи между признаками; если же он положителен – о прямой связи. Если он равен нулю, то связи между признаками нет, а если равен 1, то между признаками существует не корреляционная, а функциональная связь. Перевод числового значения коэффициента корреляции в характеристики тесноты связи осуществляется в соответствии со шкалой Чэддока (табл.8.5). Таблица 8.5 Шкала Чэддока [12]
Для расчета линейного коэффициента корреляции пользуются следующей формулой:
где
где r – линейные коэффициенты корреляции, а подстрочные знаки показывают, между какими признаками они исчисляются. Другим важным показателем корреляционно-регрессионного анализа является коэффициент детерминации (r2), который представляет собой коэффициент корреляции, возведенный в квадрат. Он показывает, какая доля вариации результативного признака обеспечивается за счет вариации конкретного факторного признака. Здесь необходимо иметь в виду, что при использовании корреляционно-регрессионного анализа для практических целей необходимо, чтобы значение коэффициента детерминации было достаточно большим, обеспечивающим более 50% вариации результативного признака. При разработке многофакторных моделей важным этапом является проверка существенности отличия от нуля коэффициента множественной корреляции. Коэффициент множественной корреляции показывает тесноту связи зависимой величины со всей совокупностью факторов-аргументов. Проверка существенности отличия от нуля коэффициента множественной корреляции позволяет проверить всю регрессионную модель. Если окажется, что коэффициент множественной корреляции существенно от нуля не отличается, то можно сделать вывод о равенстве нулю всех коэффициентов регрессии и забраковать всю модель. Простейшим методом проверки существенности коэффициента множественной корреляции является построение для него доверительных интервалов и выяснение вопроса о том, находится нуль внутри построенного интервала. Доверительный интервал для коэффициента множественной корреляции R определяется по формуле R - tsR £ R £ R + tsR, (8.17) где sR - средняя квадратическая ошибка R; t - критерий Стьюдента (обычно принимается t = 2). Среднюю квадратическую ошибку коэффициента множественной корреляции находят по формуле
где n - количество наблюдений в анализируемой выборке (группе); р - число факторных признаков в уравнении множественной регрессии. Для проверки существенности коэффициента множественной корреляции также можно применять F-критерий, который определяется по формуле
при р и n - p - 1 степенях свободы. Применение уравнения множественной регрессии в практических целях в стандартизированном масштабе затруднительно, а поэтому его следует перевести в натуральный масштаб. Коэффициенты множественной регрессии из стандартизированного в натуральный масштаб переводятся по формуле
где bi – коэффициенты уравнения множественной регрессии в натуральном масштабе; bi – коэффициенты уравнения множественной регрессии в стандартизированном масштабе; sy – среднее квадратическое отклонение результативного признака; sxi – среднее квадратическое отклонение xi – го факторного признака. Кроме проверки значимости всей модели необходимо также проверить значимость каждого из коэффициентов регрессии. Проверка производится по t- критерию Стьюдента, при этом минимальная величина коэффициента регрессии должна соответствовать условию
В формуле bi – коэффициент уравнения множественной регрессии в натуральном масштабе при xi – м факторном признаке; sbi – средняя квадратическая ошибка bi – го коэффициента, которая определяется по формуле
где sy – среднее квадратическое отклонение результативного признака у; sxy – среднее квадратическое отклонение xi – го факторного признака; R – коэффициент множественной корреляции уравнения регрессии; Ri – коэффициент множественной корреляции xi – го факторного признака с другими факторными признаками (без результативного фактора у); n – число наблюдений. Если коэффициент уравнения множественной регрессии в натуральном масштабе при каком-нибудь из факторных признаков окажется несущественным (обычно если t < 2), его следует из уравнения регрессии исключить и все расчеты начать сначала. После окончательного уточнения коэффициентов уравнения множественной регрессии в натуральном масштабе находят значение свободного члена уравнения регрессии в натуральном масштабе по формуле
где На основе данных корреляционного регрессионного анализа можно определить совместное и раздельное влияние факторных признаков на результативный признак. Влияние вариации каждого факторного признака в отдельности на вариацию результативного признака определяет частный коэффициент детерминации, который показывает, какая доля общей вариации результативного признака у вызывается именно вариацией данного фактора xi. Частные коэффициенты детерминации рассчитывают по формуле
где di – частный коэффициент детерминации факторного признака xi; bi – коэффициент множественной регрессии в стандартизированном масштабе при факторном признаке xi; ryxi – парный коэффициент корреляции между результативным признаком у и факторным признаком xi. Влияние отдельных факторных признаков на результативный признак в едином масштабе можно определить по частным коэффициентам эластичности, которые характеризуют, на сколько процентов (долю процента) изменится уровень результативного признака у при изменении xi – го факторного признака на 1%. Частный коэффициент эластичности определяется по формуле
где Эi – частный коэффициент эластичности; bi – коэффициент уравнения множественной регрессии в натуральном масштабе при xi – м факторном признаке;
Важным показателем, отражающим качество модели, является среднее квадратическое отклонение оценок результативного признака, рассчитанных по уравнению регрессии, от их фактических значений (стандартная ошибка оценок), которая определяется по формуле
где n – число наблюдений в выборке; р – число факторных признаков модели. Данная величина является показателем абсолютного отклонения оценок. По нему можно определить коэффициент вариации модели по формуле
где V – коэффициент вариации модели, %;
|

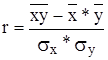 (8.15)
(8.15) – среднее значение произведения х на у;
– среднее значение произведения х на у;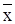 и
и  – среднее значение соответствующих признаков;
– среднее значение соответствующих признаков; и
и  – средние квадратические отклонения, найденные по признаку х и по признаку у.
– средние квадратические отклонения, найденные по признаку х и по признаку у.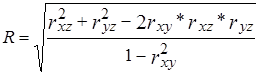 , (8.16)
, (8.16) , (8.18)
, (8.18) , (8.19)
, (8.19) (8.20)
(8.20) . (8.21)
. (8.21) , (8.22)
, (8.22)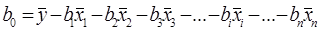 , (8.23)
, (8.23) - средние значения признаков.
- средние значения признаков.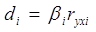 , (8.24)
, (8.24) , (8.25)
, (8.25) - среднее значение xi – го факторного признака;
- среднее значение xi – го факторного признака; - среднее значение результативного признака.
- среднее значение результативного признака. , (8.26)
, (8.26) - стандартная ошибка оценок;
- стандартная ошибка оценок; , (8.27)
, (8.27) - среднее значение результативного признака.
- среднее значение результативного признака.


