Теория вопроса.
Группа: ЭО-12
Вологда
Цель работы:определить коэффициент вязкости и длину свободного пробега молекул воздуха. Оборудование:стеклянный сосуд с краном, пробка с капилляром, штатив, мерный стакан (колба), линейка, вода.
Теория вопроса.
Тепловое хаотическое движение молекул газа способствует сглаживанию всяких различий между равными частями газа. Поэтому если мы имеем слои газа, движущиеся с различными по величине скоростями, то на упорядоченное движение слоев газа с различными скоростями накладывается хаотическое движение молекул. Молекулы переходят из слоя, движущегося со скоростью
Этот закон можно вывести, используя основные положения молекулярно-кинетической теории. Пусть у нас имеются два слоя газа, движущиеся со скоростями Количество движения, переносимое потоком молекул в положительном направлении оси Z из слоя, движущегося со скоростью
где Количество движения, переносимое потоком молекул в противоположном направлении, равно:
Изменение импульса слоя
Учитывая, что
то выражение (2) примет вид:
Известно, что изменение импульса тела определяется импульсом силы:
В полученном выражении силы произведение
Впредлагаемом методе определения динамического коэффициента вязкости используется истечение воздуха через капилляр. Известно, что скорости истечения бесконечно тонких цилиндрических слоев воздуха, расположенных на различных расстояниях от оси капилляра, различны и распределены по сечению капилляра по параболическому закону. Наибольшая скорость будет на осевой линии капилляра, и, по мере приближения к стенкам, скорость уменьшается, а слой, прилегающий к стенке, неподвижен, т.е. “прилипает” к ней. Между слоями, движущимися с различными скоростями, возникает сила внутреннего трения (сила вязкости). При установившемся движении сила вязкости, действующая на элементарный объем и приложенная к боковой поверхности цилиндра, уравновешивает разность сил давлении, действующих на основание цилиндра. На концах капилляра при протекании по нему воздуха возникает разность давлений (
Здесь r – радиус капилляра;
Учитывая, что давление у верхнего конца капилляра равно атмосферному, разность давлений на концах капилляра выразиться:
Поскольку, в процессе опыта давление столба воды уменьшается (за счет истечения), то берут среднее значение:
и выражение для вязкости примет вид:
Если учесть, что
Здесь P – атмосферное давление; R – газовая постоянная;
|

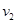 , в слой движущийся со скоростью
, в слой движущийся со скоростью 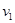 , и обратно, перенося при этом импульс. Такой процесс переноса количества движения (импульса), выравнивающий скорости отдельных слоев, сопровождается превращением кинетической энергии упорядоченного движения данного слоя в энергию теплового движения молекул и называется внутренним трением. Закон Ньютона для внутреннего трения имеет вид:
, и обратно, перенося при этом импульс. Такой процесс переноса количества движения (импульса), выравнивающий скорости отдельных слоев, сопровождается превращением кинетической энергии упорядоченного движения данного слоя в энергию теплового движения молекул и называется внутренним трением. Закон Ньютона для внутреннего трения имеет вид:
 (1)
(1)
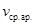 – средняя арифметическая скорость.
– средняя арифметическая скорость.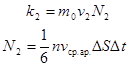
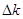 выразиться:
выразиться: (2)
(2) (плотность вещества), а разность скоростей
(плотность вещества), а разность скоростей  можно выразить через градиент скорости и длину свободного пробега
можно выразить через градиент скорости и длину свободного пробега 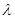 :
: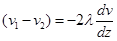
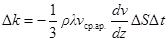 (3)
(3) , тогда сила трения будет равна:
, тогда сила трения будет равна: (4)
(4)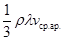 представляет собой динамический коэффициент вязкости:
представляет собой динамический коэффициент вязкости: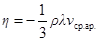 (5)
(5) входа –
входа – 
 (6)
(6) – динамический коэффициент вязкости;
– динамический коэффициент вязкости; 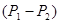 – разность давлений в начале капилляра и в конце; l – длина капилляра; V – объем газа, протекшего через сечение капилляра за время t.
– разность давлений в начале капилляра и в конце; l – длина капилляра; V – объем газа, протекшего через сечение капилляра за время t. Таким образом, для определения коэффициента вязкости достаточно измерить разность давлений, время истечения газа, его объем, радиус и длину капилляра.
Таким образом, для определения коэффициента вязкости достаточно измерить разность давлений, время истечения газа, его объем, радиус и длину капилляра. Схема установки представлена на рис. 2 и состоит из стеклянного сосуда А со шкалой. Верхняя часть сосуда закрыта пробкой с капилляром, а в нижней имеется трубка с краном К. Перед началом работы кран закрыт, сосуд заполнен водой на
Схема установки представлена на рис. 2 и состоит из стеклянного сосуда А со шкалой. Верхняя часть сосуда закрыта пробкой с капилляром, а в нижней имеется трубка с краном К. Перед началом работы кран закрыт, сосуд заполнен водой на  объема и плотно закрыт пробкой с капилляром. Если открыть кран k, то по истечении некоторого времени вода из сосуда А будет вытекать каплями. При объем воды, вытекающий из сосуда, равен объему воздуха, прошедшего через капилляр, а давление у открытого конца трубки D равно сумме давлений: воздуха, находящегося над поверхностью воды в сосуде А, и гидростатического давления
объема и плотно закрыт пробкой с капилляром. Если открыть кран k, то по истечении некоторого времени вода из сосуда А будет вытекать каплями. При объем воды, вытекающий из сосуда, равен объему воздуха, прошедшего через капилляр, а давление у открытого конца трубки D равно сумме давлений: воздуха, находящегося над поверхностью воды в сосуде А, и гидростатического давления  ,
, 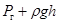 . Это давление уравновешивается атмосферным
. Это давление уравновешивается атмосферным 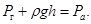
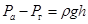
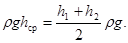
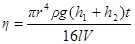 (7)
(7) , а
, а 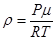 , то для средней длины свободного пробега молекул получим выражение:
, то для средней длины свободного пробега молекул получим выражение: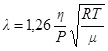 (8)
(8)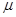 – молярная масса.
– молярная масса.


