Теоретическое введение. 1 Ознакомиться с эффектом холла.
Лабораторная работа №67 ИЗУЧЕНИЕ ЭФФЕКТА ХОЛЛА В ПРОВОДНИКАХ
Цель работы 1 Ознакомиться с эффектом холла. 2 Определить постоянную Холла. 3 Измерить концентрацию носителей тока в полупроводнике.
Теоретическое введение
Эффект Холла, открытый в 1879 году, заключается в возникновении в металле или полупроводнике с током плотностью Поместим металлическую или полупроводниковую пластинку с током плотностью
Для выбранного направления
где а – высота пластинки. Сила тока согласно классической электронной теории электропроводности вычисляется по формуле
где S – площадь поперечного сечения пластинки шириной d, n – концентрация электронов, v – средняя скорость их упорядоченного движения). Выразив из (1) Δ φ; и подставив в формулу для разности потенциалов скорость v из (2) получим:
где Рассмотренный вывод холловской постоянной является весьма приближенным, так как не учитывает скорость хаотического движения электронов. Более строгое выражение можно записать в виде:
где А – постоянная, зависящая от механизма рассеяния носителей заряда. Для полупроводника с носителями одного знака она изменяется в пределах 1,17 ≤ А ≤ 1,93. В настоящей работе используется полупроводник, для которого с достаточной степенью точности можно принять значение А = 1,17. Для полупроводника с двумя типами носителей постоянная Холла равна
где nn и np - концентрация электронов и дырок, un и up – их подвижности. В зависимости от типа носителей и их подвижностей знак постоянной Холла может быть как «+» так и «-» что позволяет не спутать в эксперименте эффект Холла с другими возможными эффектами, не зависящими от направления тока. С этой целью при измерении холловской разности потенциалов Δ φ; меняют направление
|


 , помещенном в магнитном поле
, помещенном в магнитном поле  , электрического поля в направлении, перпендикулярном
, электрического поля в направлении, перпендикулярном  .
.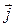 в магнитное поле с индукцией
в магнитное поле с индукцией  , направленное перпендикулярно
, направленное перпендикулярно  (рисунок 1).
(рисунок 1).
 , искривляющая их траекторию. В данном случае сила Лоренца направлена вверх. Таким образом, у верхнего края пластинки возникает повышенная концентрация электронов (он зарядится отрицательно), а у нижнего – их недостаток (он зарядится положительно). В результате возникает направленное вертикально вверх электрическое поле
, искривляющая их траекторию. В данном случае сила Лоренца направлена вверх. Таким образом, у верхнего края пластинки возникает повышенная концентрация электронов (он зарядится отрицательно), а у нижнего – их недостаток (он зарядится положительно). В результате возникает направленное вертикально вверх электрическое поле  . Когда действие этого поля на заряды уравновесит действие силы Лоренца, установится стационарная разность потенциалов Δ φ; между верхней и нижней гранями пластин (Холловская разность потенциалов).
. Когда действие этого поля на заряды уравновесит действие силы Лоренца, установится стационарная разность потенциалов Δ φ; между верхней и нижней гранями пластин (Холловская разность потенциалов). , (1)
, (1) , (2)
, (2) , (3)
, (3) - постоянная Холла.
- постоянная Холла. , (4)
, (4) , (5)
, (5) . (6)
. (6)


