Бинарные деревья
Бинарные деревья являются деревьями со степенью не более двух. Бинарное (двоичное) дерево – это динамическая структура данных, представляющее собой дерево, в котором каждая вершина имеет не более двух потомков (рис. 31.3). Таким образом, бинарное дерево состоит из элементов, каждый из которых содержит информационное поле и не более двух ссылок на различные бинарные поддеревья. На каждый элемент дерева имеется ровно одна ссылка.
Каждая вершина бинарного дерева является структурой, состоящей из четырех видов полей. Содержимым этих полей будут соответственно:
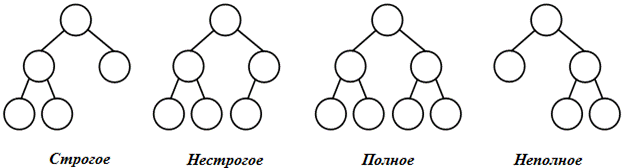
По степени вершин бинарные деревья делятся на (рис. 31.4):
В общем случае у бинарного дерева на k -м уровне может быть до 2k-1 вершин. Бинарное дерево называется полным, если оно содержит только полностью заполненные уровни. В противном случае оно является неполным. Дерево называется сбалансированным, если длины всех путей от корня к внешним вершинам равны между собой. Дерево называется почти сбалансированным, если длины всевозможных путей от корня к внешним вершинам отличаются не более, чем на единицу. Бинарное дерево может представлять собой пустое множество. Бинарное дерево может выродиться в список (рис. 31.5).
Структура дерева отражается во входном потоке данных так: каждой вводимой пустой связи соответствует условный символ, например, '*' (звездочка). При этом сначала описываются левые потомки, затем, правые. Для структуры бинарного дерева, представленного на следующем рисунке 6, входной поток имеет вид: ABD*G***CE**FH**J**.
Бинарные деревья могут применяться для поиска данных в специально построенных деревьях (базы данных), сортировки данных, вычислений арифметических выражений, кодирования (метод Хаффмана) и т.д.
struct имя_типа { информационное поле; [служебное поле;] адрес левого поддерева; адрес правого поддерева; }; где информационное поле – это поле любого ранее объявленного или стандартного типа; адрес левого (правого) поддерева – это указатель на объект того же типа, что и определяемая структура, в него записывается адрес следующего элемента левого (правого) поддерева. Например: struct point { int data;//информационное поле int count; //служебное поле point *left;//адрес левого поддерева point *right;//адрес правого поддерева }; Основными операциями, осуществляемыми с бинарными деревьями, являются:
Для описания алгоритмов этих основных операций используется следующее объявление: struct BinaryTree{ int Data; //поле данных BinaryTree* Left; //указатель на левый потомок BinaryTree* Right; /указатель на правый потомок }; .......... BinaryTree* BTree = NULL; Приведем функции перечисленных основных операций при работе с бинарным деревом. //создание бинарного дерева void Make_Binary_Tree(BinaryTree** Node, int n){ BinaryTree** ptr;//вспомогательный указатель srand(time(NULL)*1000); while (n > 0) { ptr = Node; while (*ptr!= NULL) { if ((double) rand()/RAND_MAX < 0.5) ptr = &((*ptr)->Left); else ptr = &((*ptr)->Right); } (*ptr) = new BinaryTree(); cout << "Введите значение "; cin >> (*ptr)->Data; n--; } }
//печать бинарного дерева void Print_BinaryTree(BinaryTree* Node, int l){ int i; if (Node!= NULL) { Print_BinaryTree(Node->Right, l+1); for (i=0; i< l; i++) cout << " "; printf ("%4ld", Node->Data); Print_BinaryTree(Node->Left, l+1); } else cout << endl; }
//прямой обход бинарного дерева void PreOrder_BinaryTree(BinaryTree* Node){ if (Node!= NULL) { printf ("%3ld",Node->Data); PreOrder_BinaryTree(Node->Left); PreOrder_BinaryTree(Node->Right); } }
//обратный обход бинарного дерева void PostOrder_BinaryTree(BinaryTree* Node){ if (Node!= NULL) { PostOrder_BinaryTree(Node->Left); PostOrder_BinaryTree(Node->Right); printf ("%3ld",Node->Data); } }
//симметричный обход бинарного дерева void SymmetricOrder_BinaryTree(BinaryTree* Node){ if (Node!= NULL) { PostOrder_BinaryTree(Node->Left); printf ("%3ld",Node->Data); PostOrder_BinaryTree(Node->Right); } }
//вставка вершины в бинарное дерево void Insert_Node_BinaryTree(BinaryTree** Node,int Data) { BinaryTree* New_Node = new BinaryTree; New_Node->Data = Data; New_Node->Left = NULL; New_Node->Right = NULL; BinaryTree** ptr = Node;//вспомогательный указатель srand(time(NULL)*1000); while (*ptr!= NULL) { double q = (double) rand()/RAND_MAX; if (q < 1/3.0) ptr = &((*ptr)->Left); else if (q > 2/3.0) ptr = &((*ptr)->Right); else break; } if (*ptr!= NULL) { if ((double) rand()/RAND_MAX < 0.5) New_Node->Left = *ptr; else New_Node->Right = *ptr; *ptr = New_Node; } else{ *ptr = New_Node; } }
//удаление вершины из бинарного дерева void Delete_Node_BinaryTree(BinaryTree** Node,int Data){ if ((*Node)!= NULL){ if ((*Node)->Data == Data){ BinaryTree* ptr = (*Node); if ((*Node)->Left == NULL && (*Node)->Right == NULL) (*Node) = NULL; else if ((*Node)->Left == NULL) (*Node) = ptr->Right; else if ((*Node)->Right == NULL) (*Node) = ptr->Left; else { (*Node) = ptr->Right; BinaryTree ** ptr1; ptr1 = Node; while (*ptr1!= NULL) ptr1 = &((*ptr1)->Left); (*ptr1) = ptr->Left; } delete(ptr); Delete_Node_BinaryTree(Node,Data); } else { Delete_Node_BinaryTree(&((*Node)->Left),Data); Delete_Node_BinaryTree(&((*Node)->Right),Data); } } }
//проверка пустоты бинарного дерева bool Empty_BinaryTree(BinaryTree* Node){ return (Node == NULL? true: false); }
//освобождение памяти, выделенной под бинарное дерево void Delete_BinaryTree(BinaryTree* Node){ if (Node!= NULL) { Delete_BinaryTree(Node->Left); Delete_BinaryTree(Node->Right); delete(Node); } } Листинг. (html, txt)
|



 Описание бинарного дерева выглядит следующим образом:
Описание бинарного дерева выглядит следующим образом:


