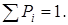Пример задачи по выбору решения
Выбрать вариант решения из «дерева решений» при следующих исходных данных: дано «дерево решений» (рис. 2) с указанными ценностями решений и вероятностями их достижения. На представленном рисунке возможен выбор одного решения из девяти. Решение приведено в табл. 1.

Рис. 2. «Дерево решений» D 9
Для каждого варианта решения рассчитывается эффективность решения. При заданных ценностях каждого из вариантов решения и вероятности его достижения эффективность решения подсчитывается по формуле
где
Единственное решение ищется следующим образом. Для i -й точки (А, В, С, D)ценность выбирается как максимальная из g -х, принадлежащих к одной точке ответвления с Рi- йвероятностью достижения:
Эффективность подсчитывается по формуле
При этом соблюдается условие (5)
Для k- хточек (М и N) процедура расчета Эk та же. Далее проводится анализ, начиная с вершины «дерева». Анализ заключается в выборе той «ветки», в вершине которой лежит точка с наибольшей эффективностью. Остальные «ветви» не рассматриваются («отрубаются»). Далее процедура повторяется до того момента, когда для рассмотрения остается одна неотрубленная «ветвь». Она и является искомым решением.
Таблица 1. Решение задачи
Далее проводится анализ, начиная с вершины «дерева» (точка О). Сравнивая ценности точек М и N выбираем «ветку» ON, поскольку ЭN = 0,66 > Эм = 0,52. «Ветка» (ОМ) отрубается полностью, и варианты А, В и 1-5 далее не рассматриваются. Сравнивая эффективности точек C и D, выбираем «ветку» ND, поскольку ЭD = 1,1 > Эс = 0,9. «Ветка» NC отрубается полностью, и варианты 6 и 7 далее не рассматриваются. Из оставшихся вариантов выбирается вариант 9 как имеющий наибольшую эффективность. О твет: вариант 9.
|

 Для каждого варианта решения (1-9) рассчитываются эффективность решения (столбец 4) по зависимости (1). Для i- й точки (А, В, С, D) ценность выбирается как максимальная из g -х, принадлежащих к одной точке ответвления (столбец 5) с Рi -й вероятностью достижения по зависимости (2). Ценность точек М и N выбирается же, как максимальная из ценности принадлежащих им «ветвей».
Для каждого варианта решения (1-9) рассчитываются эффективность решения (столбец 4) по зависимости (1). Для i- й точки (А, В, С, D) ценность выбирается как максимальная из g -х, принадлежащих к одной точке ответвления (столбец 5) с Рi -й вероятностью достижения по зависимости (2). Ценность точек М и N выбирается же, как максимальная из ценности принадлежащих им «ветвей».



 (1)
(1)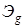 - эффективность решения; в примере g меняется от 1 до 8;
- эффективность решения; в примере g меняется от 1 до 8; 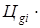 — ценность g-го решения, принадлежащего к i -й точке ответвления «дерева»; Рg — вероятность достижения этого решения. При этом соблюдается условие
— ценность g-го решения, принадлежащего к i -й точке ответвления «дерева»; Рg — вероятность достижения этого решения. При этом соблюдается условие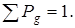 (2)
(2)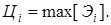 (3)
(3)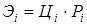 (4)
(4)