I. ПРОСТІ ЧИСЛА
ВСТУП Виникнення чисел у житті не випадковість. Важко уявити собі спілкування без використання чисел. Історія чисел захоплююча й загадкова. Людство встановило низку законів і закономірностей світу чисел. Без чудової науки про числа – математики – немислимо сьогодні минуле, ні майбутнє. А скільки ще нерозгаданого! "Найдавніші з походження числа – натуральні. "Струмки" натуральних чисел, зливаючись, породжують безмежний океан речовинних різного роду особливих спеціальних чисел", так писав про числа Б.А.Кордемський у своїй книжці "Дивний світ чисел". Особливої актуальності набувають питання, присвячені вивченню чисел Мерсенна, а саме їх зв'язок з критерієм простоти Люка – Кемера та питання постулата Бертрана. Моя робота заснована на аналізі доступних мені джерел: ресурси мережі Internet та наукова література з алгебри та теорії чисел. Об᾽єкт: прості числа. Предметом дослідження є властивості простих чисел та їх розподіл. Функція Мета роботи полягає у вивченні властивостей простих чисел і застосування їх на практиці, вивчення алгоритму пошуку кількості простих чисел на проміжку. У відповідності з метою сформульовані завдання роботи: 1. Вивчити властивості натуральних чисел. 2. Розглянути застосування простих чисел на практиці. 3. Встановити низку властивостей, законів і закономірностей різних видів простих чисел. 4. Навчитися шукати кількість простих чисел на проміжку. Основними методами дослідження простих чисел є вивчення та обробка літературних джерел, систематизація даних за видами простих чисел та їх властивостями. Робота буде корисна магістрантам, студентів старших курсів та викладачам, які цікавляться алгеброю та теорією чисел. I. ПРОСТІ ЧИСЛА 1. Означення простого та взаємно-простого числа. Деякі теореми про прості числа. Взаємно прості числа — натуральні або цілі числа, які не мають спільних дільників більших за 1, або, інакше кажучи, якщо їх найбільший спільний дільник дорівнює 1. Таким чином, 2 і 3 — взаємно прості, а 2 і 4 — ні (діляться на 2). Будь-яке натуральне число взаємно просте з 1. Якщо p — просте, а n — довільне ціле число, то вони взаємно прості тоді і тільки тоді, коли n не ділиться на p. Взаємна простота великих чисел може бути перевірена і доведена чи спростована за допомогою алгоритму Евкліда. Число 1 має тільки один дільник, а саме 1, а кожне натуральне число а, відмінне від 1, має принаймні два дільники: 1 і а (тут і далі мова йде тільки про додатні дільники). Означення 1.1 Відмінне від 1 натуральне число а називають простим, якщо воно не має дільників, відмінних від 1 і а. Його називають складеним, якщо воно має дільники, відмінні від 1 і а. Простими є, наприклад, числа 2, 7, 13; числа 4, 9, 15 – складені. Число 1 не належить ні до простих, ні до складених чисел. Доведемо кілька важливих теорем про прості числа. Теорема 1.1 Всяке натуральне число а або ділиться на дане просте число р, або взаємно просте з р. □ Справді, найбільший спільний дільник (а, р) як дільник числа р може дорівнювати або р, або 1. У першому випадку a ділиться на р, у другому а і р – взаємно прості числа. ■ Теорема 1.2 Якщо добуток кількох натуральних чисел ділиться на просте число р, то принаймні один із співмножників ділиться на р. □ Справді, внаслідок попередньої теореми, кожен із співмножників або взаємно простий з р, або ділиться на р. Але якби всі множники були взаємно прості з р, то за теоремою їх добуток був би взаємно простий з р. Тому хоч один з множників ділиться на р. ■ Теорема 1.3 Найменший відмінний від 1 дільник більшого від 1 натурального числа а є число просте. □ Нехай q – найменший дільник натурального числа а > 1. Якби q було числом складеним, то воно мало б дільник q1, такий, що 1< q1 < q. Але тоді а ділилося б на q1 і q не було б найменшим дільником числа а. ■ Теорема 1.4 Найменший відмінний від 1 дільник складеного числа а не більший за □ Нехай найменшим відмінним від 1 дільником числа а є q. Тоді а = q • a1 де а1 – деяке натуральне число, причому а1 ≥ q, бо в противному разі q не було б найменшим додатним дільником числа а. Отже, а • a1 ≥ qa1 • q і тому а ≥ q2, q ≤;
|

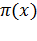 .
. 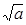 .
.


