Групповая, внутригрупповая, межгрупповая и общая дисперсия
Если выборка разбита на ряд групп, то можно вычислить групповые дисперсии. Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней
где Внутригрупповой дисперсией называют среднюю арифметическую дисперсий, взвешенную по объемам групп
где j - номер группы, Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней
где j - номер группы, Общей дисперсией называют дисперсию всех значений признака относительно общей средней
Теорема 20.1. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:
|
– частота значений 
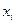, j - номер группы, 
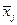- групповая средняя, 
- объем группы j.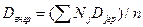
,
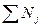- объем выборки.
,
.
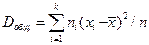
