Упорядоченные деревья

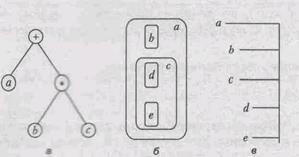
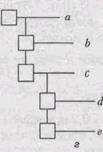
Множества Т₁,..., Т_k в эквивалентном определении ордерева являются поддеревьями. Если относительный порядок поддеревьев Т₁,..., Т_k фиксирован, то ордерево называется упорядоченным.

Пример

Ориентированные и упорядоченные ориентированные деревья интенсивно используются в программировании.

1. Выражения. Для представления выражений языков программирования, как правило, используются ориентированные упорядоченные деревья. Пример представления выражения а+b*с показан на рис. 9.7, а.

2. Для представления блочной структуры программы и связанной с ней структуры областей определения идентификаторов часто используется ориентированное дерево (может быть, неупорядоченное, так как порядок определения переменных в блоке в большинстве языков программирования считается несущественным). На рис. 9.7.б показана структура областей определения идентификаторов а, b, с, d е, причем для отображения иерархии использованы вложенные области.

3. Для представления иерархической структуры вложенности элементов данных и/или операторов управления часто используется техника отступов, показанная на рис. 9.7, в.

4. Структура вложенности каталогов и файлов в современных операционных системах является упорядоченным ориентированным деревом. Обычно для изображения таких деревьев применяется способ, показанный на рис. 9.7, г.

5. Различные «уравновешенные скобочные структуры» (например (а(b)(с(d)(е)))) являются ориентированными упорядоченными деревьями.

 

Рис. 9.7. Примеры изображения деревьев в программировании

Отступление

Тот факт, что большинство систем управления файлами использует ориентированные деревья, отражается даже в терминологии — «корневой каталог диска».

Замечание

Общепринятой практикой при изображении деревьев является соглашение о том, что корень находится наверху и все стрелки дуг ориентированы сверху вниз, поэтому стрелки можно не изображать. Таким образом, диаграммы свободных, ориентированных и упорядоченных деревьев оказываются графически неотличимыми, и требуется дополнительное указание, дерево какого класса изображено на диаграмме. В большинстве случаев это ясно из контекста.

 

Пример

На рис. 9.8 приведены три диаграммы деревьев, которые внешне выглядят различными. Обозначим дерево слева — (1), в центре — (2) и справа — (3). Как упорядоченные деревья, они все различны: (1) ≠ (2), (2) ≠ (3), (3) ≠ (1). Как ориентированные деревья (1) = (2), но (2) ≠ (3). Как свободные деревья, они все изоморфны: (1) = (2) = (3).

 

Рис. 9.8. Диаграммы деревьев