End for
Обоснование Код Прюфера действительно является представлением свободного дерева. Чтобы убедиться в этом, покажем, что если Т' — дерево, построенное алгоритмом 9.2 по коду А, который построен алгоритмом 9.1 по дереву Т, то Т' изоморфно Т, Т' ~ Т. Для этого установим отображение f: 1..р → 1..р между номерами вершин в деревьях Т, и Т' по порядку выбора вершин в алгоритмах: если вершина v выбрана на i -ом шаге алгоритма 9.1, то вершина f(v) выбрана на i -ом шаге алгоритма 9.2. Заметим, что Dom f = 1..р, поскольку висячие вершины есть в любом дереве и удаление висячей вершины оставляет дерево деревом. Далее, Iт f = 1..р, поскольку на i -ом шаге алгоритма 9.2 использовано i - 1 число из р чисел и остаётся р – i + 1 чисел, а в хвосте кода Прюфера занято не более р – i чисел. Более того, Итак, f - тождественное и, значит, взаимно-однозначное отображение. Заметим теперь, что для определения i -ого элемента кода на i -ом шаге алгоритма 9.1 используется, а затем удалется ребро (v, А[i]) и в точности то же ребро добавляется в дерево Т' на i -ом шаге алгоритма 9.2. Следовательно, f - взаимно-однозначное отображение, сохраняющее смежность и Т ~ Т'.
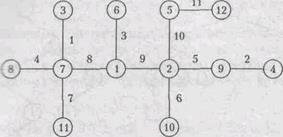
Пример Для дерева, представленного на рис. 9.10, код Прюфера 7, 9, 1, 7, 2, 2, 7, 1, 2, 5, 12. На этом рисунке числа в вершинах - это их номера, а числа на рёбрах указывают порядок, в котором будут выбираться висячие вершины и удаляться рёбра при построении кода Прюфера.
Рис. 9.10. Построение кода Прюфера
Замечание Код Прюфера — наиболее экономное по памяти представление дерева. Его можно немного улучшить, если заметить, что существует всего одно дерево с двумя вершинами — К2, а потому информацию о «последнем ребре» можно не хранить, она восстанавливается однозначно.
|
v f(v) = v. Действительно, номера вершин, которые являются висячими в исходном дереве, не появляются в коде Прюфера (кроме, может быть, одной висячей вершины с наибольшим номером), а номера вершин, которые не являются висячими, обязательно появляются. Поскольку при выборе первой вершины v в алгоритме 9.1 все вершины с меньшими номерами не являются висячими, их номера будет присутствовать в коде и, значит, не могут быть использованы на первом шаге алгоритма 9.2. Таким образом, на первом шаге алгоритм 9.2 выберет ту же вершину v. Но после удаления вершины v на втором шаге снова имеется дерево, к которому применимы те же рассуждения.
