Свободные деревья
Лекция № 15
ДЕРЕВЬЯ
Одним из простейших классом графов являются деревья. Граф является деревом, если он удовлетворяет следующей теореме. Теорема. Для графа G= <X,U> следующие утверждения эквивалентны: 1) G - дерево; 2) любые две вершины в графе G соединены единственной простой цепью; 3) граф G связен и имеет |X| - 1 ребер; 4) граф G не содержит циклов и имеет |X| - 1 ребер; 5) граф G не содержит циклов, но добавление ребра между любыми двумя несмежными вершинами приводит к появлению одного цикла; 6) граф G связен, но утрачивает это свойство после удаления любого ребра.
Деревья широко применяются в программировании.
Свободные деревья Граф без циклов называется ациклическим, или лесом. Связный ациклический граф называется (свободным) деревом. Компонентами связности леса являются деревья. Граф G, в котором q(G) = р(G)- 1, называется древовидным. В ациклическом графе G z(G) = 0. Пусть и, v — несмежные вершины графа G, х = (и, v) Пример На рис. 9.1 показаны диаграммы всех различных (свободных) деревьев с 5 вершинами, а на рис. 9.2 — диаграммы всех различных (свободных) деревьев с 6 вершинами.
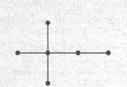
Рис. 9.1. Свободные деревья с 5 вершинами
Рис. 9.2. Свободные деревья с 6 вершинами Основные свойства деревьев Следующая теорема устанавливает, что два из четырех свойств — связность, ацикличность, древовидность и субцикличность — характеризуют граф как дерево. Теорема Пусть G(V, Е) — граф с р вершинами, q ребрами, k компонентами связности и z простыми циклами. Пусть далее х — ребро, соединяющее любую пару несмежных вершин в G. Тогда следующие утверждения эквивалентны: 1. G — дерево, то есть связный граф без циклов, k(G) = 1&z(G) = 0; 2. любые две вершины соединены в G единственной простой цепью,
3. G — связный граф, и любое ребро есть мост,
4. G — связный и древовидный,
6. G — ациклический и субциклический,
7. G — связный, субциклический и неполный,
8. G — древовидный и субциклический (за двумя исключениями),
Доказательство [1
Рис. 9.3. К доказательству теоремы о свойствах деревьев [2 [3
[4 [5
Но q=p-1, следовательно, k = 1. [5 [6 [7 [7 [8
но q' = p' -1, следовательно. k = 1. то есть дерево одно. Если в этом дереве сбединить несмежные вершины, то получим второй цикл. Два исключения: деревья, которые не имеют несмежных вершин, — это К1 и K2. Общая схема доказательства представлена на рис. 9.4. Граф доказательства сильно связен, следовательно, теорема доказана.
Вычисление
От противного Рис. 9.4. Схема доказательства теоремы о свойствах деревьев Следствие 1 В любом нетривиальном дереве имеются по крайней мере две висячие вершины. Доказательство Рассмотрим дерево G(V, Е). Дерево — связный граф, следовательно, Далее от противного. Пусть 2q = Уd(vi) > 2(р - 1) + 1 = 2р - 1. Но q = р - 1, то есть 2q = 2р - 2. Имеем противоречие: 2р - 2 2 > 2р - 1. Следствие 2. Каждая не висячая вершина свободного дерева является точкой сочленения. Доказательство Пусть G(V, Е) — дерево, v Центр дерева Свободные деревья выделяются из других графов тем, что их центр всегда оправдывает своё название. Теорема Центр свободного дерева состоит из одной вершины или из двух смежных вершин: Z(G) = 0&k(G) = 1 → С(G) = К1 Доказательство Для деревьев К1 и К2 утверждение теоремы очевидно. Пусть теперь G(V,Е) — некоторое свободное дерево, отличное от К1 и К2. Рассмотрим граф G'(V',Е'), полученный из G удалением всех висячих вершин. Заметим, что G ' — дерево, поскольку ацикличность и связность при удалении висячих вершин сохраняется. Далее, если эксцентриситет еG(v) = d(v,и), то и — висячая вершина в дереве G (иначе можно было бы продолжить цепь «за» вершину и ). Поэтому
Ориентированные, упорядоченные и бинарные деревья Ориентированные (упорядоченные) деревья являются абстракцией иерархических отношений, которые очень часто встречаются как в практической жизни, так и в математике и программировании. Дерево (ориентированное) и иерархия — это равнообъёмные понятия.
|
E. Если граф G+x имеет только один простой цикл, z(G+х)= 1, то граф G называется субциклическим.
.
;
;
;
;
;
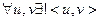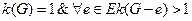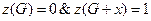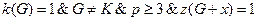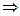2] От противного. Пусть существуют две цепи <и, v>; (рис. 9.3, слева). Тогда w, w2 — простой цикл.
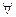и, v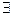 
!, следовательно, 
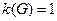. Далее от противного. Пусть ребро х — не мост. Тогда в G - х концы этого ребра связаны цепью. Само ребро х — вторая цепь.
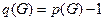для всех связанных графов G с числом вершин меньше р, у которых любое ребро суть мост. Тогда удалим из G ребро х (которое является мостом). Получим две компоненты G ' и G ";, удовлетворяющие индукционному предположению. Имеем:
.
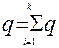i = У(pi-1) = Уpi-k = p-k
К3, G ≠ К1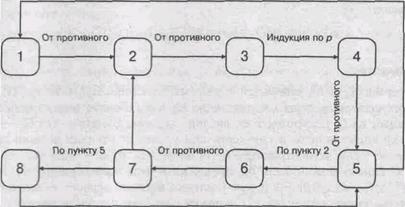 
.
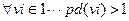. Тогда
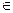V и d(v) >; 1. Тогда 
С(G) = К2.
