Ориентированные деревья

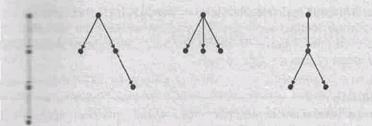
Ориентированным деревом (или ордеревом, или корневым деревом ) называется орграф со следующими свойствами.

1. Существует единственный узел r, полу степень захода которого равна 0, d⁺(r) = 0. Он называется корнем ордерева.

2. Полустепень захода всех остальных узлов равна 1, v V \ { r } d⁺(r) = 1 == 1.

3. Каждый узел достижим из корня, v V \ { r } <v, u >;.

Пример

На рис. 9.5 приведены диаграммы всех различных ориентированных деревьев с 3 узлами, а на рис. 9.6 показаны диаграммы всех различных ориентированных деревьев с 4 узлами.

Теорема. Ордерево обладает следующими свойствами:

1. q = р - 1;

2. если в ордереве забыть ориентацию дуг, то получится свободное дерево;

3. в ордереве нет контуров

4. для каждого узла существует единственный путь, ведущий в этот узел из корня;

5. подграф, определяемый множеством узлов, достижимых из узла v, является ордеревом с корнем v (это ордерево называется поддеревом узла v);

6. если в свободном дереве любую вершину назначить корнем, то получится ордерево.

рис. 9.5. Ориентированные деревья с 3 узлами

Рис. 9.6. Ориентированные деревья с 4 узлами

Доказательство

1. Каждая дуга входит в какой-то узел. Из п. 2 определения 9.2.1 имеем:

v V \ { r } d⁺(r) = 1, где r — корень. Следовательно, q = р - 1.

2. Пусть G — ордерево, граф G ' получен из G забыванием ориентации рёбер, r — корень. Тогда v₁, v₂ V (v₁, r) G' & (r, v₂) G', следовательно, v₁, v₂ (v₁, v₂) и граф G' связен. Таким образом, учитывая п. 4. теоремы 9.1.2, G' -дерево.

3. Следует из пункта 2.

4. От противного. Если бы в G существовали два пути из и в v, то в G' имелся бы цикл.

5. Пусть G_v — правильный подграф, определяемый множеством узлов, достижимых из v. Тогда d_Gv⁺(v) = 0, иначе узел v был бы достижим из какого-то узла v' G_v, и, таким образом, в G_v, а значит, и в G имелся бы контур, что противоречит пункту 3. Далее имеем: v' G_v\ { v } d⁺(v') = 1, так как G_v G. Все узлы G_v достижимы из v по построению. По определению 9.2.1 получаем, что G_v — ордерево.

6. Пусть вершина r назначена корнем и дуги последовательно ориентированы «от корня» обходом в глубину. Тогда d⁺(r) = 0 по построению;

v V - d⁺(v) = 1, так как входящая дуга появляется при первом посещении узла; все узлы достижимы из корня, так как обход в глубину посещает все вершины связного графа. Таким образом, по определению 9.2.1 получаем ордерево.

 

СЛЕДСТВИЕ Алгоритм поиска в глубину строит ордерево с корнем в начальном узле.