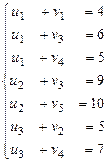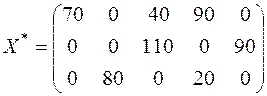Шаг 1.Определение потенциалов поставщиков и потребителей.На этом шаге составляем систему уравнений для потенциалов, используя только занятые клетки. Используем последний опорный план:
Заметим, что в этой системе всего 8 неизвестных, т.е. m + n (3 + 5). Однако уравнений всего 7, поскольку в невырожденном опорном плане всего 7 заполненных клеток (т.е. m + n - 1). Для однозначного решения не хватает одного уравнения. В этом случае один из потенциалов, например, и 1 (может быть и другой потенциал) приравнивают некоторому постоянному числу, например, нулю: и 1=0. Это и будет недостающим уравнением в системе. Теперь систему можно легко решить, имея в виду, что все уравнения состоят только из двух неизвестных. Результаты решения записаны в заголовочных клетках таблицы. Решать систему можно и непосредственно по таблице, используя занятые клетки с известными значением одного из потенциалов. Этот процесс всегда можно начать с первой строки, где уже известно значение и 1=0. Сделаем замечание для случая, когда опорный план является вырожденным. В этом случае количество уравнений для определения потенциалов будет меньше, чем m + n – 1. Это недопустимо мало, поэтому используют следующий приём. В недостающее число свободных клеток записывают нулевые значения перевозок, а сами эти клетки считаются занятыми, и для них записывают уравнения потенциалов. Такая модификация опорного плана не влияет на его стоимость, поскольку нулевые перевозки имеют нулевую стоимость. Свободные клетки значащих нулей для подстановки выбираются не произвольно, однако об этом поговорим ниже.
Шаг 2. Проверка оптимальности опорного плана. На этом шаге проверяем выполнение неравенств (7) для свободных клеток. Перепишем их в виде:
Если все S ij неотрицательны, значит, опорный план оптимален, и на этом наш вычислительный процесс заканчивается. Подсчитаем оценки для свободных клеток: S 12 = 11 – (0 - 1) = 12 ³ 0 S 15 = 15 – (0 +7) = 8 ³ 0 S 21 = 8 – (3 + 4) = 1 ³ 0 S 22 = 7 – (3 - 1) = 5 ³ 0 S 24 = 13 – (3 + 5) = 5 ³ 0 S 31 = 10 – (6 + 4) = 0 ³ 0 S 34 = 7 – (6 + 5) = - 4 < 0 S 35 = 20 – (6 + 7) = 7 ³ 0 Оценка S 34 оказалась отрицательной, значит, одно из неравенств (7) нарушено, и опорный план не является оптимальным. Таким образом, он нуждается в модификации, которую проведем на следующем этапе. Шаг 3. Пересчет по циклу. Для пересчета плана выбирается клетка, в которой оказалась отрицательная оценка. Таких клеток может оказаться несколько. В этом случае для пересчета выбирается клетка с самой отрицательной оценкой. Циклом в опорном плане транспортной задачи называется замкнутый многоугольник из клеток таблицы с прямыми углами в вершинах, в который входят только вершинные клетки, и все эти клетки, кроме одной (для которой организуется пересчет, т.е. с отрицательной оценкой), являются занятыми.
 Таким образом, одна из клеток цикла является свободной. Циклы могут иметь бесконечно много конфигураций, например:
В последнем случае место пересечения двух линий цикла не входит в сам цикл, поскольку в вершинах цикла, которые, собственно, только и входят в цикл, совершается поворот на 90 0. Каждой вершине цикла присваивается знак плюс или минус. При этом начальная клетка цикла, котороя является свободной, имеет знак плюс. Остальные клетки имеют чередующиеся знаки. Поскольку очевидно, что любой цикл имеет четное число вершин, то количество отрицательных и положительных вершин всегда будет одинаковым. В данном случае цикл пойдет через клетки (А 3, В 4); (А 1, В 4); (А 1, В 3) и (А 3, В 3). В таблице цикл обрисован пунктирным прямоугольником. Одним из признаков опорного плана транспортной задачи является то обстоятельство, что для любой свободной клетки всегда можно построить замкнутый цикл, где все остальные вершины будут располагаться в занятых клетках. Однако такой цикл будет единственным. С другой стороны, в опорном плане нельзя построить замкнутый цикл, в который входили бы только занятые клетки. Это привело бы к противоречивой системе уравнений для потенциалов. Данное замечание подсказывает правило, по которому в вырожденный опорный план должны быть помещены значащие нули: их нельзя располагать в клетках, которые могут создать замкнутый цикл только из занятых клеток. Отсюда следует, что, если в транспортной задаче число занятых клеток превышает m + n – 1, то из них можно построить замкнутый цикл, и план уже не будет опорным. Теперь вернемся к построенному нами циклу. Из всех отрицательных вершин цикла выбираем наименьшее значение перевозок:
Далее на значение
Пересчитаем стоимость нового плана: F (X 4 ) = 4 × 70 + 6 × 40 + 5 × 90 + 9 × 110 + 10 × 90 + 5 × 80 + 7 × 20 = 3400. Как видим, стоимость перевозок уменьшилась. Шаг 4. Определение потенциалов в новом плане. Этот шаг является повторением шага 1. Система уравнений здесь почти не отличается от предыдущей, кроме одного уравнения. Это связано с тем, что свободная клетка (А 3, В 4) стала занятой, а клетка (А3, В3) стала свободной. Фактически здесь идет речь о преобразовании однократного замещения, которое имело место в симплекс-методе. Соответственно одно из уравнений для потенциалов заменяется другим. Запишем новую систему:
Решаем эту систему аналогично, результаты помещены в заголовочные клетки последней таблицы. Шаг 5. Расчет оценок для свободных клеток. Этот шаг повторяет шаг 2. Считаем оценки: S 12 = 11 – (0 + 3) = 8 ³ 0 S 15 = 15 – (0 +7) = 8 ³ 0 S 21 = 8 – (3 + 4) = 1 ³ 0 S 22 = 7 – (3 + 3) = 1 ³ 0 S 24 = 13 – (3 + 5) = 5 ³ 0 S 31 = 10 – (2 + 4) = 4 ³ 0 S 33 = 12 – (2 + 6) = 4 ³ 0 S 35 = 20 – (2 + 7) =11 ³ 0 Поскольку все оценки свободных клеток неотрицательны, полученный план является оптимальным. В противном случае пришлось бы продолжать шаги 1-3 процесса до тех пор, пока не будет получен оптимальный план. Запишем решение транспортной задачи:
F min = F (X* ) = 3400.
|
ПН
ПО
А 2 u 2=3
, 
; 
.
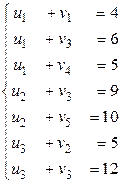
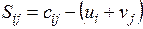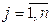уменьшаем перевозки в отрицательных вершинах цикла, а во всех положительных вершинах значения перевозок увеличиваем на эту же величину. Поскольку в цикле чётное число вершин, то в пределах цикла общий объём перевозок не изменится, что не приведет к нарушению баланса между запасами и заявками. Пересчитанная таблица выглядит так:
ПН
ПО
