МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
ОСНОВНЫЕ ПОЛОЖЕНИЯ Молекулярная физика изучает круг явлений, объяснение которых может быть дано исходя из движения и взаимодействия молекул. Методом молекулярной физики является молекулярно-кинетическая теория, основные положения которой гласят: 1) вещества состоят из мельчайших частиц, атомов или молекул, которые находятся в непрерывном, хаотическом движении; 2) в любом, даже очень малом объеме, к которому еще можно применить выводы молекулярно-кинетической теории, число частиц очень велико; 3) размеры частиц малы по сравнению с расстояниями между ними; 4) соударения частиц между собой и со стенками сосуда являются абсолютно упругими; 5) при отсутствии внешних сил частицы распределяются по всему занятому объему равномерно; 6) по абсолютной величине скорости движения частиц могут изменяться от бесконечно малых до бесконечно больших. Первая задача, которую мы рассмотрим, состоит в определении величины давления газа на стенки сосуда.
Основное уравнение молекулярно-Кинетической теории газа (уравнение Клаузиуса 1857г.)
Выделим на стенке сосуда элементарную площадку ΔS (рис.1) и подсчитаем число соударений с ней за время Δt. Очевидно, оно равно числу молекул, которые за время Δt успеют долететь до элемента ΔS. Скорости молекул будут самыми различными как по величине, так и по направлению. Кроме того, они непрерывно меняются при каждом столкновении друг с другом. Однако, если при неизменных внешних условиях сумма их кинетических энергий - величина постоянная. Так что убывание скорости одной молекулы приводит к возрастанию скорости другой. Принимая во внимание огромное число таких процессов можно считать, что распределение скоростей по значениям постоянно.
Тогда условно можно считать, что вдоль любой из осей движется 1/3 молекул, причем половина (т.е. 1/6 от общего числа) - в одну сторону, а вторая половина - в противоположную. Применим эти рассуждения к прямому цилиндру, построенному на элементе ΔS как основании. Рассматривая движение в направлении нормали к ΔS как движение вдоль одной из осей координат (X, Y или Z), получим для числа частиц, имеющих скорость ui и достигших элемента стены ΔS за время Δt:
где ni - число молекул i-ого сорта в единице объема, т.е. таких, которые имеют скорость ui; ∆Ѕ∙υi∙∆t - объем той части цилиндра, в которой содержатся молекулы i-ого сорта, способные долететь до элемента ∆Ѕ за время ∆t. При соударении каждая такая молекула массой m изменяет свой импульс на величину
∆(mυi) = - mυi- mυi = -2 mυi (2).
Тогда, в соответствии с третьим законом Ньютона, стенка получает при единичном соударении импульс силы fi∙∆t = 2mυi, а суммарный импульс, переданный молекулами i-ого сорта элементу ∆Ѕ за время ∆t:
fi∙∆t = ∆ni ∙2mυi =
Умножим и разделим правую часть равенства на 2:
fi∙∆t = т.к. Полный импульс силы, переданный площадке ∆Ѕ за время ∆t всеми молекулами, будет представлять собой сумму выражений вида (4), записанных для частиц, двигающихся со скоростями υ1, υ2, … υi … υn:
f∆t =
Разделив правую и левую часть (5) на ∆Ѕ∆t, получим:
p = Это и есть основное уравнение МКТ, которое гласит: давление идеального газа равно 2/3 кинетической энергии поступательного движения частиц в единице объема. Рассмотрим другие формы представления основного уравнения МКТ. Введем понятие о средней кинетической энергии молекулы идеального газа как
Здесь p = или с учетом (8):
Найдем взаимосвязь pVμ =
Сопоставляя (11) с уравнением состояния для моля идеального газа - pVμ = RT, имеем RT =
Здесь
Формула (12) позволяет сделать очень важный вывод: абсолютная температура идеального газа прямо пропорциональна средней энергии поступательного движения частиц. как оказывается, этот вывод справедлив не только для газов, но и для любых других агрегатных состояний вещества. Подставим в (9)
p =
Откуда n =
Для любого газа при одних и тех же значениях p и Т концентрация молекул одинакова. Например, при нормальных условиях n = 2,69∙1025 м-3 - число Лошмидта. Для смеси газов можно представить (13) в виде
p = nkT = kT но nikT = pi - это так называемое парциальное давление - давление, которое создавал бы газ i-ого сорта, если бы в сосуде был он один. T.o. давление смеси газов равно сумме парциальных давлений соответствующих компонентов Р = Р1 + Р2 + Р3… = Получим выражение для
|

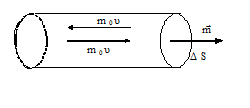 Воспользуемся моделью идеального газа: размеры его молекул столь малы, что их суммарным объемом можно пренебречь по сравнению с объемом сосуда; подавляющую часть времени каждая молекула движется свободно и лишь иногда испытывает упругие столкновения с другими молекулами и стенками сосуда. При ударе о стенку молекула передает ей некоторый импульс силы – FmΔtm, численно равный изменению количества движения молекулы – Δ(mυ). Каждый элемент поверхности стенки ΔS непрерывно подвергается "бомбардировке" большим количеством молекул, что и создает силовое воздействие, т.е. давление, со стороны молекул на стенку, которое направлено по нормали к ней.
Воспользуемся моделью идеального газа: размеры его молекул столь малы, что их суммарным объемом можно пренебречь по сравнению с объемом сосуда; подавляющую часть времени каждая молекула движется свободно и лишь иногда испытывает упругие столкновения с другими молекулами и стенками сосуда. При ударе о стенку молекула передает ей некоторый импульс силы – FmΔtm, численно равный изменению количества движения молекулы – Δ(mυ). Каждый элемент поверхности стенки ΔS непрерывно подвергается "бомбардировке" большим количеством молекул, что и создает силовое воздействие, т.е. давление, со стороны молекул на стенку, которое направлено по нормали к ней. Любое движение в пространстве можно рассматривать как движение вдоль трех взаимно перпендикулярных осей: OX, OY, OZ, независимо, как эта система сориентирована. В силу хаотичности вероятность движения молекул вдоль любого направления одинакова.
Любое движение в пространстве можно рассматривать как движение вдоль трех взаимно перпендикулярных осей: OX, OY, OZ, независимо, как эта система сориентирована. В силу хаотичности вероятность движения молекул вдоль любого направления одинакова.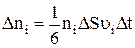 (1),
(1),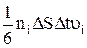 ∙2mυi =
∙2mυi = 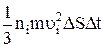 (3).
(3).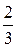 ni ∙
ni ∙ 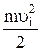 ∙∆Ѕ∙∆t =
∙∆Ѕ∙∆t =  (4),
(4),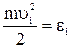 - кинетическая энергия поступательного движения одной частицы, движущейся скоростью υi.
- кинетическая энергия поступательного движения одной частицы, движущейся скоростью υi.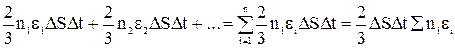
 (5).
(5).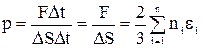 (6).
(6). - представляет собой суммарную кинетическую энергию молекул в единице объема, т.е. объемную плотность энергии поступательного движения. Обозначим
- представляет собой суммарную кинетическую энергию молекул в единице объема, т.е. объемную плотность энергии поступательного движения. Обозначим 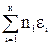 =w. Теперь (6) примет вид:
=w. Теперь (6) примет вид: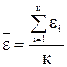 . Тогда
. Тогда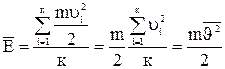 (8).
(8).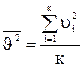 - называется средней кинетической скоростью частиц (следует иметь ввиду, что
- называется средней кинетической скоростью частиц (следует иметь ввиду, что 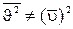 ). Теперь w =
). Теперь w = 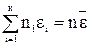 и (7) примет вид:
и (7) примет вид: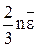 (9),
(9),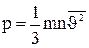 (10).
(10).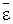 с макропараметрами идеального газа. Умножим (9) на молярный объем Vμ:
с макропараметрами идеального газа. Умножим (9) на молярный объем Vμ: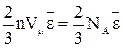 (11).
(11).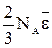 , что дает:
, что дает: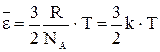 (12).
(12).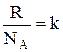 - постоянная Больцмана, k = 1,38∙10-23 Дж/К.
- постоянная Больцмана, k = 1,38∙10-23 Дж/К.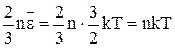 (13).
(13).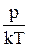 .
.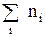 = n1kT + n2kT + n3kT + … nikT + …,
= n1kT + n2kT + n3kT + … nikT + …,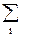 Рi (14) - закон Дальтона.
Рi (14) - закон Дальтона.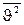 через макропараметры идеального газа: Из (12)
через макропараметры идеального газа: Из (12) 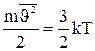 , тогда
, тогда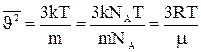 ;
; 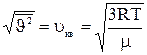 (15).
(15).


