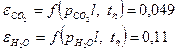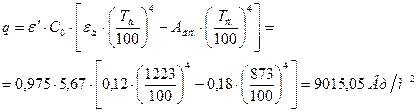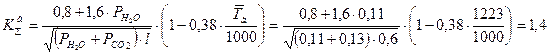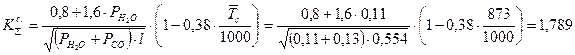МАГНИТОГОРСК
Кафедра ТиЭС КУРСОВАЯ РАБОТА ПО ТЕПЛОМАССООБМЕНУ
МАГНИТОГОРСК Задача 1. Нестационарная теплопроводность
Металлическая заготовка, имеющая форму пластины (циллиндра), неограниченной длинны, с начальной температурой 1. Время нагревания заготовки до данной конечной температуры; 2. Температуры на оси и на поверхности заготовки для различных моментов времени (с использование монограмм Будрина); 3. Распределение температуры по толщине заготовки для четырёх моментов времени (с использованием аналитических формул); 4. Количество теплоты, подведённой к телу в течении всего периода нагревания (на 1 5. По результатам (2) и (3) построить графики.
Форма тела: ПЛАСТИНА Материал: СТАЛЬ 08КП
1._Определение времени нагревания заготовки до конечной температуры Сначала найдем из справочных таблиц теплофизические параметры пластины (теплоёмкость, коэффициент теплопроводности, коэффициент температуропроводности и плотность) при начальной температуре
Вычислим число
По номограмме Будрина для центра пластины определим:
Вычислим время нагревания заготовки:
2._Определение температур на оси и на поверхности заготовки для различных моментов времени
Интервал времени нагревания заготовки разобьём на несколько промежутков. Для каждого значения
Для 1. Время нагревания
2. Безразмерная температура в центре пластины (определяем по соответствующей диаграмме Будрина в зависимоси от
3. Безразмерная температура на поверхности пластины (определяем по соответствующей диаграмме Будрина в зависимоси от
4. Температура на оси циллиндра:
5. Температура на поверхности циллиндра:
Для остальных значений критерия Фурье вычисления производим по этим же формулам, результаты вычислений заносим в таблицу.
3._Определение распределения температуры по толщине заготовки для четырёх моментов времени
Для Ө=N1 · cos(μ1 · X) · е-μ12 Fo
При
Найдём температуру в момент времени 1. Аргумент косинуса (в радианах):
2. Косинус, вычисленный в этом аргументе:
3. Безразмерная температура для этой точки:
4. Температура для этой точки:
Для остальных точек и в другие моменты времени вычисления производим аналогичным образом, результаты записываем в таблицу.
4._Определение количества теплоты, подведённого к телу за весь период нагревания (в расчёте на 1 квадратный метр поверхности пластины) Полное количество теплоты, которое было бы подведено к пластине (на 1 квардратный метр её поверхности), если бы нагревание длилось до наступления полного теплового равновесия между пластиной и воздухом печи:
Средняя безразмерная температура в последний момент времени нагрева:
Полное количество теплоты, подведённого к пластине (на 1 квадратный метр её поверхности) за весь период нагрева:
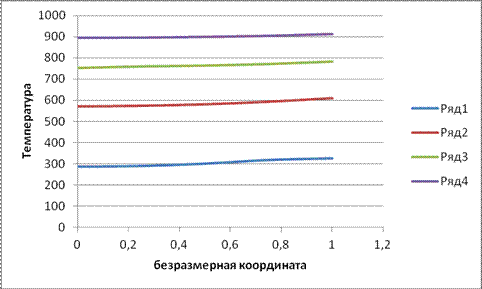
5._Графики, построенные по данным пунктов 2 и 3
Задача 2. Конвективный теплообмен при вынужденном продольном обтекании плоской поверхности
Плоская пластина 1. Критическую координату 2. Толщины динамического 3. Значения местных коэффициентов теплоотдачи 4. Средние коэффициенты теплоотдачи 5. Построить графики
Жидкость: трансформаторное масло
1. Вычисление критической координаты точки перехода ламинарного пограничного слоя в турбулентный
Определим теплофизические параметры дымовых газов при температуре
Определим число Прандтля дымовых газов при температуре
Вычислим число Рейнольдса:
Критическое число Рейнольдса:
Т.к. Вычислим координату
2. Вычисление толщин динамического и теплового пограничных слоёв на различных расстояниях от передней кромки поверхности 2.1. Расчёт ламинарного режима течения
2.1.1. Вычисление толщин динамического и теплового пограничных слоёв, а также коэффициентов теплопередачи для различных точек
Для точки
Для других точек ламинарного режима течения вычисления производим по этим же формулам, результаты записываем в таблицу.
2.1.2. Вычисление среднего коэффициента теплопередачи и плотности теплового потока
2.2. Расчёт турбулентного режима течения
2.2.1. Вычисление толщины динамического пограничных слоя, а также коэффициентов теплопередачи для различных точек
Для точки
Для других точек турбулентного режима течения вычисления производим по этим же формулам, результаты записываем в таблицу. 2.2.2. Вычисление среднего коэффициента теплопередачи и плотности теплового потока
2.3. Результаты вычислений
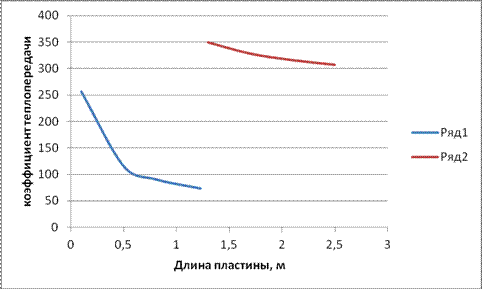
3. Построение графиков по результатам вычислений
Задача 3. Тепловой расчёт экономайзера
В экономайзер поступает вода. Вода движется по стальным трубам диаметром Определить поверхность нагрева, количество и длину змеевиков пароперегревателя парового котла. Схема движения теплоносителей в пароперегревателе показана на рисунке.
1. Вычисление внешнего диаметра трубы с учётом слоя сажи
2. Уравнение теплового баланса
Считая, что потери давления по длине парогенератора равны 0, запишем уравнение теплового баланса:
Средняя температура воды: Изобарная теплоёмкость воды:
Примем Температура дымовых газов на выходе из ПП:
Средняя температура дымовых газов:
При этой температуре теплоемкость газа:
Ср1 = 1,14 кДж/(кг·град)
Средняя температура дымовых газов:
Разности температур:
3.. Вычисление коэффициента теплоотдачи от дымовых газов к стенке
Теплофизические параметры дымовых газов:
Число Рейнольдса для дымовых газов:
1000<Re1<100000- смешанный режим движения
Число Нуссельта для дымовых газов:
Где εs= 1,2<2, εs=
Коэффициент теплоотдачи от пара к стенке:
4 Вычисление коэффициента теплоотдачи от воды к стенке
4.1Вычисление коэффициента теплоотдачи конвекцией
Теплофизические параметры воды:
Число Рейнольдса для воды:
Re2>100000- турбулентный режим
Число Нуссельта при коридорном расположении чистых труб:
Коэффициент теплопередачи конвекцией:
α1изл= tc1=tcp1=tcp1- Средняя длина пути луча:
Произведения средней длины луча на парциальные давления двуокиси углерода и водяных паров:
При tср1=376°С по графикам определяем степени черноты двуокиси углерода и водяного пара:
По графику определяем поправочный коэффициент
Суммарная степень черноты газовой смеси:
Температура поверхности труб: При По графикам определяем степени черноты двуокиси углерода и водяного пара по средней температуре стенки труб пароперегревателя
Поглощательная способность газовой смеси:
Степень черноты поверхности:
Приведённая степень черноты поверхности:
Тепловой поток, обусловленный излучением дымовых газов к стенке:
Коэффициент теплоотдачи излучением:
Коэффициент теплоотдачи на стороне дымовых газов α1=αнар=α1к+αизл=82,1+5,9=88
5. Вычисление коэффициента теплопередачи для единицы длины трубы
Уточняем значения температуры стенки tc1=tср1 -
Пересчитаем α1изл. При tc1=286°С
Коэффициент теплоотдачи излучением:
α1=αнар=α1к+αизл=82,1+4,4=86,5
6. Определение конструктивных характеристик теплообменного аппарата Общая длина труб теплообменника:
Поверхность теплообмена (используется значение наружного диаметра, т.к со стороны дымовых газов меньшее значение коэффициента теплоотдачи):
Количество труб:
Определим длину отдельных секций (змеевиков):
Задача 4. Теплообмен излучением между газом и твёрдой охлаждающей поверхностью Вычислить плотность теплового потока, обусловленного излучением дымовых газов к поверхности газохода сечением AxB. Состав газов задан. Общее давление газа
Материал: СТАЛЬ ШЕРОХОВАТАЯ
Степень черноты стали шероховатой:
Вычислим приведённую степень черноты стали шероховатой:
Вычислим среднюю температуру газов по тракту:
Средняя длинна пути луча:
Парциальные давления двуокиси углерода и водяного пара:
Первый метод (с использованием диаграмм)
Произведение парциального давления на двуокиси углерода и водяного пара на длинну луча:
По графикам определяем степени черноты двуокиси углерода и водяного пара:
По графику определяем поправочный коэффициент
Степень черноты газовой смеси:
По графикам определяем степени черноты двуокиси углерода и водяного пара по температуре стенки
Поглощательная способность газовой смеси:
Плотность теплового потока:
Второй метод (аналитический)
Суммарное парциальное давления водяного пара и двуокиси углерода:
Степень черноты газовой смеси:
Поглощательная способность газовой смеси:
Плотность теплового потока:
Литература
1. Е.И. Казанцев. Промышленные печи. 2. Е.А. Краснощёков, А.С.Сукомел. Задачник по теплопередаче. 3. Ривкин С.Л.,Александров А.А.
|

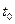 , нагревается в печи, температура которой
, нагревается в печи, температура которой 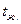 поддерживается постоянной до конечной температуры по оси заготовки
поддерживается постоянной до конечной температуры по оси заготовки  . Считая длинну (и высоту) заготовки большими большими по сравнению с толщиной, определить:
. Считая длинну (и высоту) заготовки большими большими по сравнению с толщиной, определить: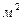 поверхности пластины или на 1
поверхности пластины или на 1  длинны циллиндра);
длинны циллиндра);

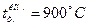

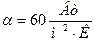
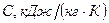
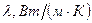


 и безразмерную температуру
и безразмерную температуру  для центра пластины в последний момент времени нагрева:
для центра пластины в последний момент времени нагрева: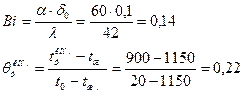
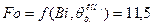
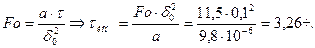
 вычислим время (в часах), найдём безразмерные температуры в центре и на поверхности пластины по номограммам Будрина (в зависимости от
вычислим время (в часах), найдём безразмерные температуры в центре и на поверхности пластины по номограммам Будрина (в зависимости от  :
: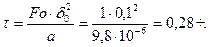

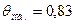
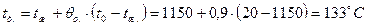

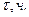
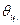
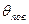
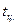

 (т.к. заготовка имеет форму пластины), для вычисления безразмерной температуры можно ограничится одним членом ряда:
(т.к. заготовка имеет форму пластины), для вычисления безразмерной температуры можно ограничится одним членом ряда:
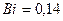 определим из таблиц:
определим из таблиц: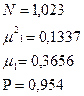
 при расстоянии от центра пластины
при расстоянии от центра пластины  :
:

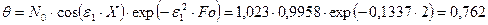

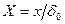
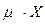


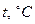

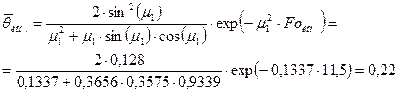

 м. обтекается продольным потоком жидкости (газа) со скоростью
м. обтекается продольным потоком жидкости (газа) со скоростью 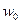 м/с. Температура набегающего потока
м/с. Температура набегающего потока 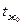 . Задана температура поверхности пластины
. Задана температура поверхности пластины 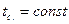 . Найти:
. Найти: точки перехода ламинарного пограничного слоя в турбулентный;
точки перехода ламинарного пограничного слоя в турбулентный; и теплового
и теплового  пограничных слоёв на различных расстояниях от передней кромки поверхности;
пограничных слоёв на различных расстояниях от передней кромки поверхности;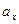 на различных расстояниях от передней кромки пластины;
на различных расстояниях от передней кромки пластины;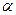 для участков с различными режимами течения;
для участков с различными режимами течения;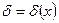 ,
, 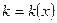 ,
,  .
.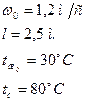
 :
: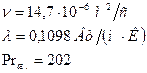
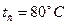 :
:

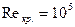
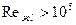 , то режим течения в пограничном слое на конце пластины - турбулентный.
, то режим течения в пограничном слое на конце пластины - турбулентный.
 вычислим:
вычислим: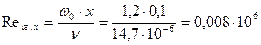
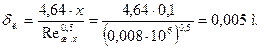



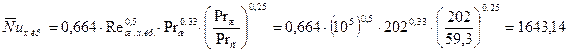


 вычислим:
вычислим: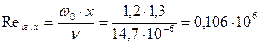

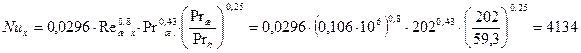



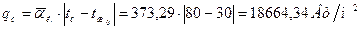





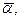
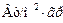
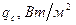

 . Коэффициент теплопроводности стали
. Коэффициент теплопроводности стали 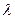 . Средняя скорость движения пара
. Средняя скорость движения пара 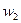 , расход пара
, расход пара  , давление
, давление  . Температура и энтальпия перегретого пара соответственно
. Температура и энтальпия перегретого пара соответственно 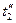 и
и 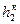 . Дымовые газы (13%
. Дымовые газы (13% 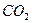 и 11%
и 11% 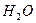 ) в количестве
) в количестве 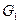 движутся вдоль трубного пучка. Температура газов на входе
движутся вдоль трубного пучка. Температура газов на входе 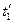 . Средняя скорость газов в узком сечении пучка
. Средняя скорость газов в узком сечении пучка 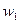 . Заданы расположение труб (шахматное или коридорное) и относительные шаги: поперечный
. Заданы расположение труб (шахматное или коридорное) и относительные шаги: поперечный 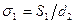 и продольный
и продольный 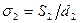 . Со стороны газов трубы пароперегревателя покрыты слоем сажи толщиной
. Со стороны газов трубы пароперегревателя покрыты слоем сажи толщиной  . Теплопроводность сажи можно принять
. Теплопроводность сажи можно принять  . Изменением давления по длинне пароперегревателя в расчётах можно пренебречь.
. Изменением давления по длинне пароперегревателя в расчётах можно пренебречь. Вода:
Вода:
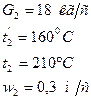
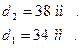 Расположение труб:
шахматное
Коэффициент теплопроводности сажи:
Расположение труб:
шахматное
Коэффициент теплопроводности сажи:
 Коэффициент теплопроводности стенки:
Коэффициент теплопроводности стенки:
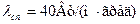
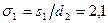 Продольный относит. шаг:
Продольный относит. шаг:
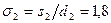 Слой сажи:
Слой сажи:
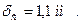 Слой накипи:
Слой накипи:




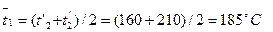

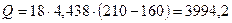 кВт
кВт , тогда
, тогда 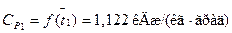
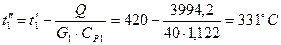

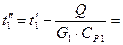
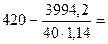 332,4°С
332,4°С
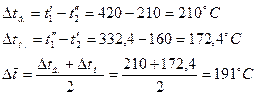

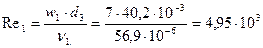


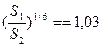
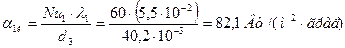


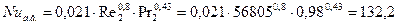

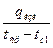
 °C
°C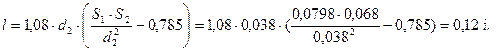

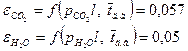
 на парциальное давление для водяного пара:
на парциальное давление для водяного пара: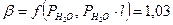


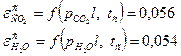
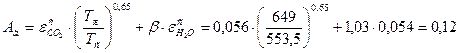
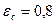


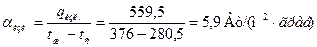
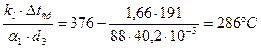
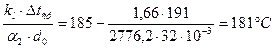


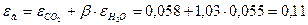
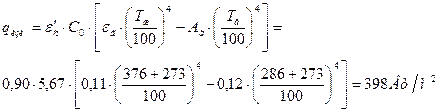



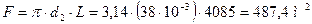

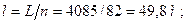
 . Температура газов на входе в газоход
. Температура газов на входе в газоход 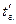 и на выходе
и на выходе 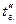 . Средняя температура поверхности газохода
. Средняя температура поверхности газохода 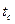 .
.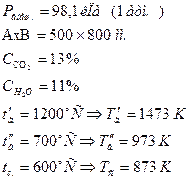

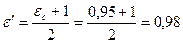
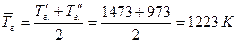
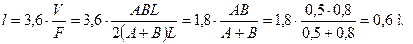


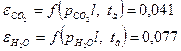

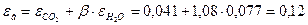
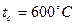 :
: