Лабораторная работа №5
Ультразвук в физике твердого тела
1. Скорость звука
Одним из методов исследования свойств твердых тел является возбуждение упругих колебаний. Традиционно упругие колебания называют ультразвуковыми колебаниями, хотя частоты колебаний в твердых телах могут на много порядков превышать диапазон частот обычно используемый в ультразвуковой технике. Основное применение ультразвука: измерение упругих констант, изучение дефектов решетки, изучение электронной структуры металлов и сверхпроводников, изучение магнитоакустических и прочих взаимодействий. Все это помимо широкого применения ультразвука в технике. Все частоты механических колебаний выше частоты слышимости человеческим ухом (свыше 20 кГц) называют ультразвуком. Источником звука может быть любое колеблющееся тело в любом агрегатном состоянии. Звуковые волны представляют собой продольные и поперечные механические колебания атомов и молекул в веществе. При этом колеблющиеся атомы образуют области сжатия и расширения которые распространяющиеся с определенной скорость. Скорость распространения упругих волн в веществе в первую очередь зависит от механических свойств среды. В изотропных твердых телах могут распространяться как поперечные (деформация сдвига), так и продольные волны (деформация сжатия). У продольных волн смещение частиц происходит в том же направлении, в котором движется волна. У поперечных волн смещение частиц перпендикулярно движению волны. Для жидкости скорость звука определяется из выражения v = (1/χ·ρ)1/2, (1.а) где χ – коэффициент сжимаемости[1]. Из механики известно, что скорость продольных волн в твердом длинном тонком стержне определяется из выражения v = (E ю/ρ)1/2, (1.б) где Е ю – модуль Юнга[2], ρ – плотность стержня. Поскольку скорость звука выражается через плотность, она зависит от температуры. Скорость звука в бесконечно тонкой пластине
где μ – коэффициент Пуассона[3]. (1.б) Данные о плотности, модуле упругости, коэффициенте Пуассона и сжимаемости приведены в таблице 1. В этой же таблице приведены и данные о скорости звука в различных материалах. Однако надо иметь в виду, что обычно в справочниках приводится скорость для случая распространения звука в безграничной среде. Тогда как скорость звука в реальном твердом теле зависит от геометрических размеров. Только для некоторых материалов скорость звука в тонких стержнях приведена в таблице 1. Как видно из приведенных формул существует общая формула, из которой в первом приближении можно определить скорость звука выглядит так: v = (1/χ'·ρ)1/2, (2) где χ' – коэффициент сжимаемости среды. Для жидкости χ' = χ – сжимаемости жидкости, а для твердых тел вид χ' зависит от размеров образца и типа волны. Дело в том, что скорость распространения продольных волн существенно зависит от соотношения между длиной волны ультразвука и поперечными размерами тела. Если длина волны существенно больше поперечных размеров образца, то поперечное распределение деформаций и напряжений происходит так же, как и при статической нагрузке: удлинение образца в продольном направлении сопровождается его сжатием в поперечном направлении. В качестве χ' в формулу (2) следует подставить 1/ Е ю. Если, наоборот, поперечные размеры образца существенно превышают длину волны, то сжатие в продольном направлении происходит при неизменных поперечных размерах. В качестве χ' в этом случае следует подставить коэффициент односторонней сжимаемости, связанный с модулем Юнга Е и коэффициентом Пуассона μ формулой
Скорость продольных волн при этом равна:
2. Распространение звука в веществе
2.1. Плоская ультразвуковая волна, движущаяся по направлению х, описывается формулой у = А sin (ωt – kx), (5) где у - смещение колеблющихся частиц, А - амплитуда смещения, ω- круговая частота колебаний, t - время, k - волновое число. Вынося k за скобку, получим у=А sin [ k (v·t – x)]. (6) В этой формуле величина v = ω/k (7) определяет скорость ультразвука в упругой среде. В обычных условиях скорость ультразвука не зависит ни от амплитуды, ни от частоты колебаний. Скорость ультразвука в воздухе составляет около 330 м/с, в воде – 1500 м/с, в кварце – 5700 м/с, в стали – 6000 м/с. Скорость движения частиц в среде не имеет ничего общего со скоростью распространения ультразвука. Скорость частиц можно найти, дифференцируя (5) по времени: V част = А ωcos (ωt – kx). (8) Как показывает формула (9), скорость частиц гармонически зависит от времени. Амплитуда их колебаний равна А ω. Найдем кинетическую энергию, отнесенную к единице объема колеблющейся среды: Е кин = ½ρ V 2част = ½ρ(А ω)2cos2(ω t – kx). (9) При гармонических колебаниях потенциальная энергия волны в среднем равна кинетической. Сумма этих энергий – полная энергия, отнесенная к единице объема (плотность энергии), равна Е полн = Е кин + Е пот = ½ρ(А ω)2.(10) Здесь мы учли, что среднее значение квадрата от косинуса равно ½. Эта энергия движется вместе с волной, т. е. перемещается со скоростью v. Поток энергии, пересекающий единичную площадку, расположенную перпендикулярно направлению распространения волны, равен J = ½ρ v (А ω)2. (11) Входящая в эту формулу величина ρ· v называется акустическим сопротивлением среды.
2.2. Исследуем прохождение ультразвуковой волны через границу раздела двух упругих сред. При нормальном падении волны на такую границу в первой среде, кроме падающей волны: y пад = А sin (ω t - k 1 x). (12) возникает отраженная волна, движущаяся навстречу падающей: y отр = В sin (ω t - k 1 x). (13) Во второй среде распространяется преломленная волна y прел = D sin (ω t – k 2 x). (14) Найдем коэффициент отражения на границе. Приравнивая смещения частиц слева и справа от границы, найдем А sin (ω t - k 1 x)+ B sin (ω t - k 1 x) = D sin (ω t - k 2 x). Пусть граница расположена при x = 0. Полагая x = 0 и сокращая равенство на sin ω t, найдем A + B = D. (15) Приравняем теперь поток энергии в падающей волне сумме потоков в преломленной и отраженной волнах: ½ρ1 v 1(А ω)2 = ½ρ1 v 1(В ω)2 + ½ρ2 v 2(D ω)2 Введем обозначение: R = ρ1 v 1/ρ2 v 2. (16) Величина R равна отношению акустических сопротивлений соседних сред. Наша формула при этом приобретает вид R (А 2 - В 2)= D 2. Деля это равенство на (16), найдем R (A - B) = D. (17) Система уравнений (16) и (18) дает
(18)
Формулы (18) определяют отражение и преломление на границе. Коэффициентом отражения волны называют отношение потоков энергии в отраженной и в падающей волне. Формулы (11) и (18) дают
Формула (19) показывает, что коэффициенты отражения при переходе ультразвука из первой среды во вторую и из второй в первую равны друг другу.
Например. Волна распространяется из воды в сталь. ρводы = 1000 кг/м3, ρстали = 7800 кг/м3, v воды = 1480 м/с, v стали = 5100 м/с. R = 0.037. Из (18) В = - 0.92 А. При переходе ультразвуковой волны из воды в сталь обратно в воду отражается 92 % энергии волны и только 8% проходит дальше. На границе сталь воздух отражается 99.9 % энергии волны. При переходе из стали в дерево R составит 14 (ρдерева = ~ 700 кг/м3, v дерева ~ 4000 м/с), тогда обратно в сталь отразится 86% энергии волны. Таким образом, если волна возбуждается в стальной болванке, которая лежит на деревянном столе, то большая часть энергии волны отразится обратно в металл. Причем если болванка имеет форму правильного параллелепипеда, то волна будет отражаться от граней пробегая туда и обратно в металле несколько раз пока не затухнет.
Ультразвуковая волна, проходя через среду, испытывает затухание. Амплитуда колебаний в плоской волне уменьшается с расстоянием по экспоненциальному закону А = А 0ехр (- α· х). (20) Коэффициент αносит название коэффициента затухания. Так как интенсивность колебаний пропорциональна квадрату амплитуды, то J = J 0ехр (–2α х). (21) Затухание ультразвука является следствием того, что часть энергии поглощается веществом, превращаясь в тепловую энергию. В жидкостях и газах поглощение обусловливается в основном вязкостью и теплопроводностью среды. Как видно из (8), в один и тот же момент времени различные элементы среды имеют разные скорости. Это различие приводит к появлению сил вязкости, аналогичных трению. Разная степень сжатия различных участков волн приводит к появлению температурного распределения в среде. Возникающая при этом теплопроводность также приводит к уменьшению энергии волны. Коэффициент затухания αсвязан с коэффициентами вязкости η и теплопроводности ξ.
где ср - удельная теплоемкость при постоянном давлении. В твердых телах на затухание ультразвука оказывает влияние структура вещества. В однородных аморфных средах и в монокристаллах затухание определяется, в основном, теплопроводностью и вязкостью. В поликристаллических средах, состоящих из большого числа мелких кристаллов, затухание ультразвука существенно зависит от отношения между длиной волны λ и размерами кристалликов d. При λ > d поглощение обуславливается главным образом теплопроводностью, а при λ < d – вязкостью среды. В обоих случаях затухание пропорционально квадрату частоты ультразвука. В тех случаях, когда λ и d соизмеримы, преобладает диффузное рассеяние ультразвука на неоднородностях поликристалла, и затухание оказывается пропорциональным √;ω. Экспериментальные данные о затухании ультразвука позволяют, таким образом, судить о структуре вещества. Приблизительно скорость звука в веществе можно определить из выражения (1), зная макроскопические параметры. Например. Скорость звука в воздухе при 20˚С равна 3,44·104 см/сек,в таких условиях при частоте звука частота 34,4 кГц длина волны в воздухе составит 1 см. Ультразвук быстро затухает в воздухе. Жидкие и твердые вещества имеют большую скорость распространения звуковых волн. Скорость звука в воде при 25˚С равна 1497 м/с. Для стального стержня можно получить из (1) и данных таб. 1: v = (Е ю/ρ)1/2 ~ (20·1010/7800)1/2 = 5060 м/с. Справочное значение 5050 м/с. При частоте ультразвука f = 34 кГц длина акустической волны для стали составит λ = v / f ~ 15 см. Для того чтобы на длине образца уложилась хотя бы одна длина волны размеры образца должны быть больше 15 см или частота ультразвука выше 34 кГц. Поэтому частота ультразвука для исследования твердых тел обычно лежит в диапазоне частот выше 100 кГц, а для исследования тонких пленок требуются частоты до десятков ГГц. В твердых телах и жидкостях ультразвук затухает слабо. Для получения механических колебаний с высокими частотами, иначе генерации ультразвука, используют пьезоэлектрические или магнитострикционные преобразователи электромагнитных колебаний в механические колебания.
3. Упругие свойства анизотропного твердого тела
При механическом воздействии твердое тело подвергается деформации. Силу под действием которой происходит деформация называют напряжением 1. Всего имеется 9 компонент напряжения, однако независимыми является только шесть компонент. Закон Гука утверждает, что если деформации твердого тела достаточно малы, то они пропорциональны механическим напряжениям, т.е. компоненты деформации являются линейными функциями компонент напряжения: e xx = S 11 X x + S 12 Y y + S 13 Z z + S 14 Y z + S 15 Z x + S 16 X y, (23) …. Всего 6 уравнений.
С другой стороны компоненты напряжений являются линейными функциями компонент деформации: X x = C 11 e xx + C 12 e yy + C 13 e zz + C 14 ey z + C 15 ez x + C 16 ex y, (24) …. Всего 6 уравнений.
Величины S 11, S 12,… называются постоянными упругой податливости, или упругими постоянными; величины С 11, С 12,… называются постоянными упругой жесткости или модулями упругости. Если на элемент объема кристалла действует сила, то уравнение движения для смещения в направлении х:
Здесь ρ – плотность, а u – компонента вектора смещения. Как видно из приведенных уравнений (23) и (24) в уравнение движения (25) войдут упругие константы S ij или С ij. Решение уравнения (25) можно получить для плоской волны (5). Очевидно, что уравнения (23), (24) и (25) в зависимости от симметрии кристалла и направления распространения волны будут иметь различное число слагаемых. В анизотропных средах, которые могут обладать в общем случае 21 независимой упругой постоянной, могут существовать в данном направлении нормали к фронту волны, три различных вектора смещения, каждый из которых связан с характерной скоростью плоской волны. Из трех волн одна аналогична продольной волне, две – поперечным волнам для случая изотропного тела. Решая эти уравнения можно получить выражения для скорости продольных и поперечных волн. Экспериментально можно определить скорость соответствующих трех волн и из этих данных найти упругие константы. Например, для кубического кристалла скорость продольной волны в направлении [111] равна v l = [1/3(C 11 + 2 C 12 + 4 C 44)/ρ]1/2. Скорость поперечной волны при тех же условиях равна v 2 = [1/3(C 11 – C 12 + C 44)/ρ]1/2. Здесь ρ – плотность материала. Тогда как в направлении [100] скорость продольной и поперечных волн соответственно равны v 1 = (C 11/ρ)1/2 и v 2 = (C 44/ρ)1/2. Постоянные упругой жесткости С ij являются важными характеристиками вещества и их экспериментальное определение или теоретический расчет является актуальной задачей. Как видно из поведенных выражений для определения упругих констант необходимо в кристалле измерить скорость распространения звуковых волн в разных кристаллографических направлениях. При это требуется возбудить в веществе как продольные так и поперечные волны.
4. Измерение скорости звука в твердых телах
Для генерации звуковых волн можно воспользоваться свойством пьезоэлектриков изменять свои размеры при наложении электрического поля. Для это применяются пьезоэлектрические преобразователи электрического поля в механические колебания. Простейший преобразователь представляет собой тонкую пластинку (< 0.5 мм) из поляризованного пьезоэлектрика. Для подачи на пьезоэлектрик электрического поля на пластинку наносят электроды, которые вместе с диэлектриком пьезоэлектрика образуют плоский конденсатор. В качестве излучателей ультразвука могут использоваться также цилиндры из пьезоэлектрика, здесь электроны нанесены на боковые поверхности цилиндров, а также толстые пластины. В последнем случае толстые пластины применяются для генерации мощных импульсов ультразвука, например для гидролокации. Другим методом получения ультразвука является основанный на магнитострикции преобразователи магнитной энергии в механические колебания с использование ферромагнитных материалов, например металлического никеля. Однако пьезоэлектрические источники ультразвука имеют ряд преимуществ перед магнитострикционными преобразователями и чаще используются на практике. Как отмечалось в лабораторной работе №4 пластика пьезоизлучателя имеет собственные частоты механических колебаний. При совпадении частоты радиочастотного поля с частотой механического колебания пластинки возникает явление резонанса. Возбудить механические колебания в пьезоизлучателе можно путем подачи на него короткого электрического импульса. Поскольку добротность пьезоэлектрического элемента как механической системы достаточно велика, то при воздействии импульсного электрического поля в таком пьезоизлучателе возникают слабо затухающие колебания. Если пластинка приведена в акустический контакт с некой средой, то колеблющаяся пластинка возбуждает в образце ультразвуковые волны. Частота этих волн равна частоте собственных колебаний пьезоэлемента. Однако вследствие наличия затухания в системе колеблющейся пластинки, которая отдает мощность в окружающую среду, в образец излучается некий достаточно короткий цуг ультразвуковых колебаний. Импульс ультразвуковых колебаний проходит от излучателя до задней стенки образца за время t` = l / v, где l – длина образца в направлении распространения ультразвуковой волны, v – скорость звука в образце. Достигнув задней стенки ультразвуковая волна частично отражается обратно в образец (рис. 1), а частично преломляется и рассеивается вне образца. Отраженное волна в виде ультразвукового эха преодолевает толщины образца за точно такое же время t`. Достигнув передней стенки колебания образца, вызывают колебания пьезоэемента, что в свою очередь приводит к наведению на обкладках пьезодатчика колебаний электрических зарядов вследствие обратного пьезоэффекта. Возникающие на обкладках пьезодатчика импульсы напряжения усиливаются и поступают на электронный осциллограф.
На экране осциллографа наблюдается пульс, отстоящий от возбуждающего импульса на интервал времени 2 t`. Однако процесс распространения ультразвуковой волны в образце на этом не заканчивается. Ультразвуковой импульс, достигнув передней стенки образца и вызвав колебания пьезодатчика отражается обратно во внутрь образца. Это импульс повторно достигает задней стенки и вновь возвращается обратно. В результате много кратного прохождения сигнал сквозь образец на осциллографе будет наблюдаться серия сигналов эха (рис. 2), амплитуда которых будет постепенно уменьшаться. Уменьшение амплитуды сигналов эха связано как с непосредственным затуханием звука в веществе, так и рассеянием акустической волны при отражении от стенок образца. Проведя измерения времени между сигналами эха можно непосредственно определить скорость звука в данном направлении кристалла. Поскольку интервал между сигналами эха t = 2 t`, то v = 2 l / t (26)
В монокристаллах скорость звука может зависеть от направления распространения в кристалле. Для более детального исследования твердых тел необходимо измерить скорость прохождения продольных поперечных волн в кристалле. Для возбуждения определенного типа волн используют специально изготовленные пьезоэлементы. Например, такие пьезоэлементы можно изготовить из кварца, вырезав пластинки кварца вдоль разных направлений в кристалле. Измерив скорость распространения различных типов волн можно найти упругие постоянные С 11, С 12, С 44 в кристалле. При таких измерениях используют один и тот же образец и одно направление распространения волны, но срез и установка излучателей должна быть различной, чтобы обеспечить заданное направление колебаний атомов образца.
Измеренная таким образом скорость ультразвука является групповой скоростью волн, которая, вообще говоря, отлична от их фазовой скорости, о которой мы говорили до сих пор. При отсутствии дисперсии (дисперсией называется зависимость фазовой скорости распространения волн от их частоты) эти две скорости равны друг другу. Затухание ультразвука определяется по уменьшению интенсивности ультразвуковой волны. Существуют различные способы измерения коэффициента затухания импульсным методом. В жидкостях и газах удобно изменять длину пробега волны, увеличивая или уменьшая расстояние между излучателем и рефлектором. Сравнивая величину отраженных импульсов на экране осциллографа при двух фиксированных расстояниях, нетрудно определить коэффициент затухания aпо формуле
немедленно следующей из (21). Преимущество описываемого метода - заключается в том, что результаты измерений не зависят от коэффициента отражения волн от задней стенки. Другой способ измерения коэффициента затухания основан на исследовании последовательных отражений ультразвука от передней и задней стенки образца. Отражающими поверхностями в твердом теле могут служить его свободные концы. Расстояние, проходимое ультразвуковым импульсом между двумя последовательными возвращениями к излучателю, равно 2 l, где l - длина тела. Расчетная формула в этом случае приобретает вид
Ослабление звука, связанное с неполным его отражением от концов образца, в этом случае не исключается и входит в ошибку измерений.
Методика измерений
Блок-схема установки приведена на рис. 3.
Высоковольтный генератор импульсов подает импульс на LC контур образованный катушкой индуктивности и конденсатором С. Конденсатор С представляет собой сам пьезоизлучатель. Катушка имеет такую индуктивность, чтобы выполнялось резонансное соотношение. Элементы схемы C 1, C 2, R, D 1 и D 2 служат для согласования и развязки участков цепи. В частности пара встречновключенных диодов защищает вход усилителя от перегрузки. На рис. 3. показан импульс возбуждения и затухающие колебания, возникающие в колебательной системе. Сразу после действия импульса затухающие колебания не позволяют регистрировать сигнал эхо. Очевидно, что для наблюдения первого сигнала эха время прохождения звука в образце должно быть больше чем время переходных процессов возникающих в системе. Поэтому для тонких образцов возможно измерение сигналов эхо для кратных отражений или при условии низкой скорости звука в этих веществах. Часто кратные отражения могут не наблюдаться из-за сильного поглощения звуковых волн или сильного рассеяния на торцах образца. В таком случае следует использовать более толстые образцы или более совершенную аппаратуру для возбуждения звука. Современные методы позволяют возбуждать колебания упругих волн в диапазоне частот до сотен ГГц. Однако в таких случаях используется специальная техника приближающая по исполнению к технике СВЧ.
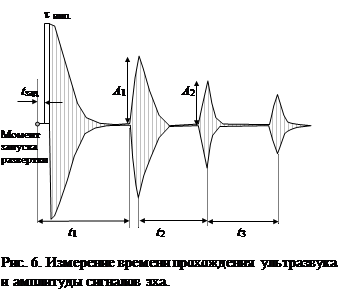
Измерение скорости звука в твердых телах имеет свои особенности. Торец излучателя и поверхность исследуемого образца в месте, где будет размещаться излучатель смачивается жидкостью, например, маслом или водой, для создания хорошего акустического контакта. Излучатель прикладывается к поверхности образца и вручную плотно притирается к поверхности. В ходе измерений излучатель удерживается на поверхности образца руками. При наличии четких сигналов эха проще всего произвести измерение времени t между максимумами эха, как это показано на рис. 6 (t 2 и t 3; t 2 = t 3). Расстояние между импульсами эхо измеряются на экране осциллографа в делениях шкалы и умножаются на соответствующее значение переключателя «Время/дел». Желательно интервал времени измерить как можно точнее. Кроме времени прохождения звука необходимо знать и толщину образца. Толщина измеряется с помощью штангенциркуля. Если наблюдается только один четкий сигнал эха, приходится проводить измерения относительно начала запуска развертки осциллографа (t 1). При этом следует внести поправки. Момент запуска развертки и появление импульса на выходе генератора не обязательно совпадают. В генераторе предусмотрена регулировка величины такой задержки. Для проведения некоторых измерений задержка t зад может быть равна нулю при других устанавливается конкретное время задержки, например 1 мкс. Поэтому при измерениях положения первого эха от величины t 1 следует вычесть величину задержки, если она не равна нулю. Так же из времени t 1 следует вычесть интервал времени примерно равный длительности импульса τимп. Длительность импульса устанавливается на панели прибора. Обычно выбирают очень короткие импульсы, например 0.1 – 0.3 мкс. Само же время t 1 измеряют от точки, которая индицирует начало запуска развертки до начала первого сигнала эха (рис.6). Кроме того от всех времен t 1, t 2, t 3 следует вычитать время t п ~ 0.6 мкс. Интервал времени t п возникает при прохождении звуком самого излучателя (см. ниже). Таким образом t = t 1 – t зад – τимр – 0.6 (мкс), а так же t = t 2 – 0.6. После внесения этих поправок полученное время t = 2 t' (26) используется при расчетах скорости звука.
Приборы и оборудование.
Конструкция ультразвукового излучателя приведена на рис. 7. Излучатель состоит из алюминиевого корпуса в нижней части которого находится пьезодатчик. Пьезодатчик залит эпоксидной смолой, которая служит для аккустической связи датчика с внешней средой. Из-за наличия конечной толщины слоя смолы (l п на рис. 7) звук в начале преодолевает слой смолы и только потом передается исследуемому материалу. Толщина слоя l п порядка 2 мм. При скорости звука в смоле примерно 3400 м/с задержка на прохождения слоя смолы составит примерно 0.6 мкс. Наличие этой задержки следует учитывать при проведении измерений (см. выше). Выводы излучателя подключены к схеме (рис. 3). В верхней части излучателя находится предварительный усилитель. Усилитель питается от источника напряжением 9 – 12 В.
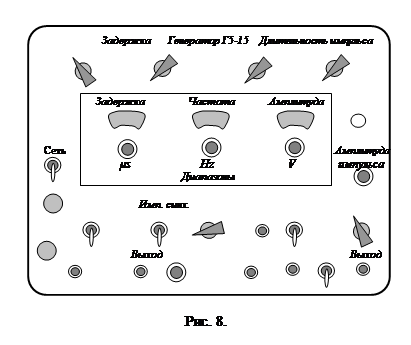
В качестве генератора импульсов используется генератор Г5-15 (рис. 8). Три ручки в верхней левой части прибора служат для установки задержки импульса относительно импульса синхронизации. Выход импульса синхронизации «Выход» расположен внизу в левой части прибора. Две ручки справа, вверху служат для установки длительности импульса. Ручки «Частота», «Hz» служат для установки частоты следования импульсов. Ручка «Амплитуда» служит для измерения амплитуды импульса. Вращая ручку «Амплитуда» добиваются зажигания лампочки расположенной справа от ручки, значение амплитуды считывают по шкале «V». Сама же амплитуда импульса регулируется ручкой «Амплитуда импульса». Выходной разъем импульса «Выход» находится справа, внизу на панели прибора.
Практическая часть Излучатель подключается к блоку питания, осциллографу и генератору. На осциллографе и генераторе ручки управления устанавливаются в исходное положение. (Про исходное положение ручек спросить у преподавателя). Приборы включаются сеть.
1. Провести измерения скорости звука в воде при трех разных расстояниях между излучателем и рефлектором. Измерить затухание звука в воде при тех же положениях рефлектора. Вычислить среднее значение скорости. Сравнить с данными приведенными в таблице 2 для скорости звука в воде при той температуре, которая имеет место в момент проведения измерений. Вычислить среднее значение затухания и сравнить табличными данными. 2. Измерить скорость звука в металлических образцах. Для одного из материалов рассчитать теоретическую скорость звука (формулы 1б и 4), пользуясь данными таблицы 1. 3. Измерить затухание звука для всех образцов. 4. Измерить скорость звука в плексигласе. Рассчитать теоретическую скорость звука (формулы 1б и 4), пользуясь данными таблицы 1. 5. Измерить затухание звука. 6. Провести измерения скорости звука для двух направлений в кристалле кварца. Одно из направлений соответствует Х -срезу, другое Y -срезу (см. работу №4). Исходя из полученных данных и плотности кварца рассчитать модуль Юнга для этих направлений. 7. Измерить затухание звука. 8. Провести измерения скорости звука для двух направлений в кристалле сапфира. Вычислить модуль Юнга для кристалла сапфира. 9. Измерить затухание звука. 10. Все полученные данные представить в виде сравнительной таблицы. Форму таблицы составить самостоятельно. На основании данных представленных в таблице сделать обобщающие выводы о механических свойствах исследованных материалов.
Таблица. 1. Модули упругости, скорость звука, плотность и сжимаемость для жидкостей и некоторых твердых веществ
Таблица 2. Скорость звука в воде при разных температурах.
[1] Коэффициент сжимаемости отношение относительного изменения объема к изменению давления, вызвавшее это изменение: χ = – d V / V ·d p.
Литература. 1. Киттель Ч. Введение в физику твердого тела. М.: 1978. Гл. 4 2. Портис А. Физическая лаборатория М.: 1972. Раздел 2.
Словарь терминов и комментарии
[2] Модуль упругости или модуль Юнга равен отношению приложенного напряжения σ к вызванному им относительному удлинению: Е ю = σ/ε, где σ = F / S, F – сила, S – площадь, ε = Δ l / l. [3] Коэффициент Пуассона равен отношению относительного изменения поперечного размера тела к относительному изменению его длины. Обычно μ принимает значения от 0.2 до 0.5..
|

 , (1.в)
, (1.в)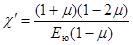 (3)
(3)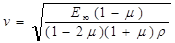 (4)
(4)
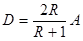
 . (19)
. (19)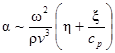 (22)
(22) (25)
(25)
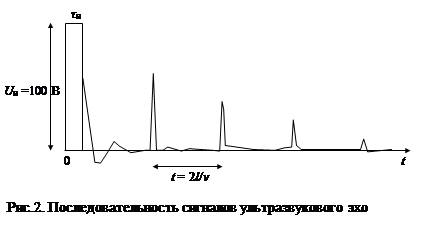
 (25)
(25)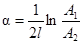 (26)
(26)
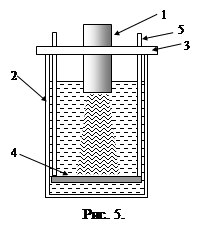 Для измерения скорости звука в воде применяется специальное устройство (рис.5) состоящее из излучателя 1, сосуда с водой 2, держателя ультразвукового излучателя 3, подвижного рефлектора 4, приспособления для подъема рефлектора 5. Ультразвук излучается погруженным в воду излучателем и отражается от рефлектора, который представляет собой металлическую пластину. Рефлектор можно поднимать и таким образом изменять глубину прохождения ультразвука. Это позволяет измерять поглощение звука в воде пользуясь формулой (25), а также наблюдать интерференцию ультразвука. Интерференция возникает, когда волна проходящая в прямом направлении встречается отраженной волной. При фиксированной частоте ультразвуковых волн можно наблюдать интерференцию, если подобрать подходящую глубину прохождения ультразвука. Глубина измеряется штангенциркулем.
Для измерения скорости звука в воде применяется специальное устройство (рис.5) состоящее из излучателя 1, сосуда с водой 2, держателя ультразвукового излучателя 3, подвижного рефлектора 4, приспособления для подъема рефлектора 5. Ультразвук излучается погруженным в воду излучателем и отражается от рефлектора, который представляет собой металлическую пластину. Рефлектор можно поднимать и таким образом изменять глубину прохождения ультразвука. Это позволяет измерять поглощение звука в воде пользуясь формулой (25), а также наблюдать интерференцию ультразвука. Интерференция возникает, когда волна проходящая в прямом направлении встречается отраженной волной. При фиксированной частоте ультразвуковых волн можно наблюдать интерференцию, если подобрать подходящую глубину прохождения ультразвука. Глубина измеряется штангенциркулем.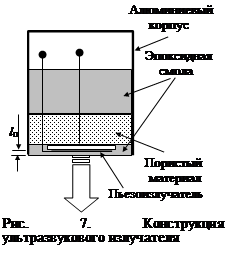 В работе используются следующие приборы: генератор импульсов Г5-15, осциллограф С1-65А, ультразвуковой излучатель, блок питания, штангенциркуль, набор образцов. Для измерения скорости звука предлагаются следующие материалы: вода, спирт (на данный момент отсутствует), цилиндры из дюралюминия, железа, латуни, бронзы, пластинка плексигласа, кристалл кварца, кристалл корунда.
В работе используются следующие приборы: генератор импульсов Г5-15, осциллограф С1-65А, ультразвуковой излучатель, блок питания, штангенциркуль, набор образцов. Для измерения скорости звука предлагаются следующие материалы: вода, спирт (на данный момент отсутствует), цилиндры из дюралюминия, железа, латуни, бронзы, пластинка плексигласа, кристалл кварца, кристалл корунда.