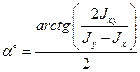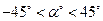Момент инерции относительно оси, параллельной центральной (теорема Штейнера)
Теорема Штейнера: Момент инерции относительно оси, параллельной центральной, равен центральному осевому моменту инерции плюс произведение площади всей фигуры на квадрат расстояния между осями.
Для прямоугольника высотой h и шириной b: Осевой момент инерции:
Момент сопротивления изгибу: момент сопротивления изгибу равен отношению момента инерции к расстоянию наиболее удаленного волокна от нейтральной линии:
т.к.
Для круга: Полярный момент инерции: Осевой момент инерции: Момент сопротивления кручению: Т.к. Момент сопротивления изгибу:
2. План выполнения расчетно-графической работы «Геометрические характеристики плоских сечений»
2.1. Выписать следующие справочные данные из раздела 3:
· для равнобокого уголка /пример обозначения №4 (4) b – ширина полки, F – площадь поперечного сечения, z 0 – координата центра тяжести,
· для неравнобокого уголка /пример обозначения №4/2,5 (4) B – ширина большей полки, b – ширина меньшей полки, F – площадь поперечного сечения, x0, y0 – положение центра тяжести
· для швеллера h – высота, b – ширина полки, F – площадь поперечного сечения, z 0 – координата центра тяжести,
· для двутавра h – высота, b – ширина полки, F – площадь поперечного сечения,
· для полосы - вычислить площадь поперечного сечения - вычислить осевые моменты инерции сечения по формулам
2.2. На миллиметровой бумаге формата А4 в выбранном Вами масштабе начертить сечение, составленное из стандартных профилей, пронумеровать: №1 – уголок, №2 – швеллер или двутавр, №3 – полоса.
2.3. Выбрать положение координатных осей. Рационально, если одна из осей проходит через центр тяжести одной из фигур, и все оставшиеся координаты центров тяжести будут положительными. Определить положение центра тяжести сечения по формулам:
Нанести положение центра тяжести на чертеж.
2.4. Определить расстояния: · между центральной осью сечения yc и осью yc1, проходящей через центр тяжести уголка
Если · между центральной осью сечения yc и осью yc2, проходящей через центр тяжести швеллера (или двутавра)
Если · между центральной осью сечения yc и осью yc3, проходящей через центр тяжести полосы
Если · между осями xc и xc1
Если · определить a2 и a3
2.5. Вычислить с помощью теоремы Штейнера осевые моменты инерции сечения по формулам:
где
в зависимости от расположения полосы по отношению к оси 0xc3. Размер стороны, перпендикулярной оси 0xc3, берется в третьей степени (в кубе). Аналогично для осевых моментов неравнобокого уголка, швеллера или двутавра – значение осевого момента из справочника берется большее, если большая сторона перпендикулярна оси 0x, и, соответственно, меньшее, если меньшая сторона перпендикулярна оси 0x F1, F2, F3 – площади поперечных сечений.
где
Центробежный момент инерции сечения:
где
Знаки a1, b1, a2, b2, a3, b3 учитываются.
2.6. Вычислить значение угла поворота α;:
Если значение угла α; положительное – оси поворачиваются против часовой стрелки.
2.7. Вычислить значение главных осевых моментов инерции
2.8. Заполнить таблицу №1.
|

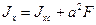



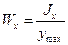
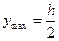 , то
, то 

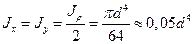

 , то
, то 

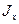 - осевой момент инерции сечения,
- осевой момент инерции сечения, - центробежный момент инерции
- центробежный момент инерции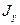 - осевые моменты инерции сечения,
- осевые моменты инерции сечения,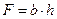
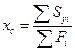 ,
, 
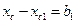
 , то b1, будет со знаком «-»
, то b1, будет со знаком «-»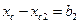
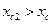 , то b2, будет со знаком «-»
, то b2, будет со знаком «-»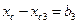
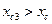 , то b3, будет со знаком «-»
, то b3, будет со знаком «-»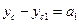
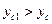 , то a1, будет со знаком «-»
, то a1, будет со знаком «-» ,
, - осевой момент инерции для уголка (указан в справочнике)
- осевой момент инерции для уголка (указан в справочнике) - осевой момент инерции швеллера или двутавра (указан в справочнике)
- осевой момент инерции швеллера или двутавра (указан в справочнике) - осевой момент инерции для полосы вычислить по формулам:
- осевой момент инерции для полосы вычислить по формулам:
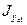 - осевой момент инерции для уголка (указан в справочнике). Для равнобокого уголка
- осевой момент инерции для уголка (указан в справочнике). Для равнобокого уголка 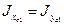 . Для неравнобокого уголка выбирается меньшее значение, если большая сторона уголка перпендикулярна оси 0xc1, а меньшая сторона уголка перпендикулярна оси 0yc1.
. Для неравнобокого уголка выбирается меньшее значение, если большая сторона уголка перпендикулярна оси 0xc1, а меньшая сторона уголка перпендикулярна оси 0yc1.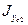 - осевой момент инерции швеллера или двутавра (указан в справочнике). Большее или меньшее значение зависит от расположения стандартного профиля по отношению к оси.
- осевой момент инерции швеллера или двутавра (указан в справочнике). Большее или меньшее значение зависит от расположения стандартного профиля по отношению к оси. - осевой момент инерции для полосы
- осевой момент инерции для полосы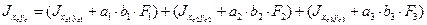
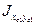 - центробежный момент инерции для уголка (берется из справочника). При расположении уголка в I и III четверти декартовой системы координат знак у центробежного момента «-», во II и в IV четверти – знак «+».
- центробежный момент инерции для уголка (берется из справочника). При расположении уголка в I и III четверти декартовой системы координат знак у центробежного момента «-», во II и в IV четверти – знак «+».
 - центробежный момент инерции для швеллера или двутавра.
- центробежный момент инерции для швеллера или двутавра. - центробежный момент инерции для полосы.
- центробежный момент инерции для полосы.