Северодвинск
Федеральное агентство по образованию Российской Федерации Филиал «СЕВМАШВТУЗ» государственного образовательного учреждения высшего профессионального образования «Санкт- Петербургский государственный морской технический университет» в г. Северодвинске
Курзанова Е.В.
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ Методические указания к выполнению расчетно-графической работы «Геометрические характеристики плоских сечений»
Северодвинск УДК 539.3/8
Сопротивление материалов. Методические указания к выполнению расчетно-графической работы по теме «Геометрические характеристики плоских сечений» /Сост. Е.В.Курзанова Северодвинск: РИО Севмашвтуза, 2008 - с.
Методические указания предназначены для студентов всех специальностей, изучающих курс «Сопротивление материалов». Методические указания по сопротивлению материалов разработаны для выполнения расчетно-графической работы по теме: «Геометрические характеристики плоских сечений». Указания содержат основные положения и зависимости рассматриваемой темы, план решения расчетно-графической работы, справочные данные для стандартных профилей.
Рецензенты: К.т.н., доцент кафедры №3 Н.В.Лобанов, начальник ЦНИЛ НТП НИТИЦ Н.П.Коломеец.
Печатается по решению редакционно-издательского совета Севмашвтуза.
© Севмашвтуз, 2008 СОДЕРЖАНИЕ Предисловие …………………………………………………………………….4
1. Основные понятия раздела «Геометрические характеристики плоских сечений» …………………………………………………………….5
2. План выполнения работы ……………………………………………….…10
3. Справочные данные для стандартных профилей проката …………….15
4. Вопросы для защиты расчетно-графической работы …….…………….31
5. Список литературы …………………………………………………………31 ПРЕДИСЛОВИЕ
Методические указания к выполнению расчетно-графической работы «Геометрические характеристики плоских сечений» В методических указаниях содержатся теоретические положения, план решения работы, справочные данные для стандартных профилей проката. Целью методических указаний является оказание помощи студентам при решении и защите расчетно-графической работы «Геометрические характеристики сечений». 1. Основные понятия раздела «Геометрические характеристики плоских сечений». К геометрическим характеристикам плоских сечений относятся: · площадь сечения F, · статические моменты площади Sx, Sy, · осевые моменты инерции Jx, Jy, · центробежный момент инерции Jxy, · полярный момент инерции Jρ , · момент сопротивления кручению Wρ, · момент сопротивления изгибу Wx
1.1. Статические моменты площади Sx, Sy
Статический момент площади равен сумме произведений элементарных площадок на расстояние до соответствующей оси.
Единицы измерения Sx и Sy: [см3], [мм3]. Знак «+» или «-» зависит от расположения осей. Sx=0 и Sy=0, если точка пересечения координатных осей совпадает с центром тяжести сечения
Пример: Определить положение центра тяжести плоского сечения, состоящего из двух прямоугольников с вырезом.
1.2. Осевые моменты инерции Jx; Jy
Осевой момент инерции равен сумме произведений элементарных площадок на квадрат расстояния до соответствующей оси.
Единица измерения [см4], [мм4]. Знак всегда «+». Не бывает равным 0. Принимает минимальное значение, когда точка пересечения координатных осей совпадает с центром тяжести сечения. Осевой момент инерции показывает, что чем дальше площадь удалена от центральной оси, тем лучше сечение сопротивляется действующей нагрузке. Осевой момент инерции сечения применяют при расчетах на прочность, жесткость и устойчивость.
1.3. Полярный момент инерции сечения Jρ
Взаимосвязь полярного и осевого моментов инерции:
Полярный момент инерции сечения равен сумме осевых моментов.
Свойство: при повороте осей в любую сторону, один из осевых моментов инерции возрастает, а другой убывает (и наоборот). Сумма осевых моментов инерции остается величиной постоянной.
1.4. Центробежный момент инерции сечения Jxy
Центробежный момент инерции сечения равен сумме произведений элементарных площадок на расстояния до обеих осей
Единица измерения [см4], [мм4]. Знак «+» или «-».
Координатные оси u и v, проходящие через центр тяжести сечения, относительно которых центробежный момент равен нулю, называются главными центральными осями инерции сечения. Главными они называются потому, что центробежный момент относительно них равен нулю, а центральными – потому, что проходят через центр тяжести сечения. У сечений, не обладающих симметрией относительно осей x или y, например у уголка,
Центробежный момент относительно осей u и v -
Формула для определения осевых моментов инерции относительно главных центральных осей u и v:
где
|


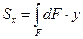







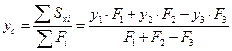
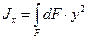
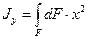

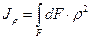
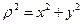

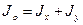

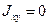 , если координатные оси являются осями симметрии (пример – двутавр), или одна из координатных осей совпадает с осью симметрии (пример – швеллер).
, если координатные оси являются осями симметрии (пример – двутавр), или одна из координатных осей совпадает с осью симметрии (пример – швеллер). не будет равен нулю. Для этих сечений определяют положение осей u и v с помощью вычисления угла поворота осей x и y
не будет равен нулю. Для этих сечений определяют положение осей u и v с помощью вычисления угла поворота осей x и y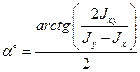
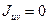

 - осевые моменты инерции относительно центральных осей,
- осевые моменты инерции относительно центральных осей,


