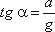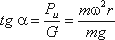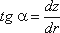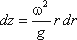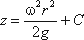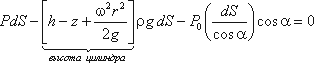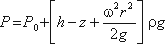Поверхности равного давления
Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. Эта поверхность горизонтальна. Свойства поверхности уровня: 1. Две различные поверхности уровня не пересекаются между собой; 2. Объемные внешние силы направлены нормально к поверхности уровня. Поверхности уровня жидкостей, соприкасающиеся с газообразной средой (чаще атмосферной), называются свободными поверхностями. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем. Рассмотрим два примера такого относительного покоя. В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.4).
Рис. 2.4. Движение цистерны с ускорением К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерции Pu, равная по величине ma. Равнодействующая
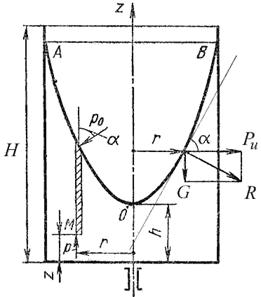
Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.4, пунктир). В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом случае (рис.2.5) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила тяжести G = mg и центробежная сила Pu = mω2r, где r - расстояние частицы от оси вращения, а ω - угловая скорость вращения сосуда.
Рис. 2.5. Вращение сосуда с жидкостью Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим
С другой стороны:
где z - координата рассматриваемой точки. Таким образом, получаем:
откуда
или после интегрирования
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C (координата вершины параболы), поэтому окончательно будем иметь
т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие поверхности уровня. Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом выведенного ранее уравнения будем иметь
После сокращений получим
Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.
|

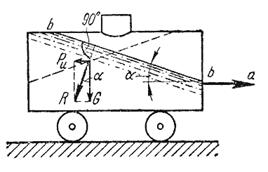
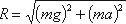 этих сил направлена к вертикали под углом α, тангенс которого равен
этих сил направлена к вертикали под углом α, тангенс которого равен