Расчет простого трубопровода.
1.Трубопровод называют простым, если жидкость транспортируется по нему от питателя к приемнику без ответвлений потока, но может иметь различные диаметры и включать местные сопротивления. Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Разность в уровнях энергии может быть обеспечена разностью уровней жидкости, работой насоса или давлением газа, например, за счет применения гидроаккумуляторов. Движение жидкости за счет разности уровней (разности геометрических высот) применяется в гидротехнике и водоснабжении. В машиностроении движение жидкости обеспечивается работой насоса и гидроаккумуляторами. Гидроаккмуляторы - емкости с разделителем, с одной стороны, использующие давление газа для создания запаса энергии, с другой стороны, рабочую жидкость, заправленную в гидроаккумулятор и находящуюся под действием давления газа. На рис.13.1 изображен простой трубопровод постоянного сечения расположенный произвольно в пространстве, состоящий из нескольких участков с длиной li и диаметром di и содержащий местные сопротивления.
В сечении «1 – 1» геометрическая высота равна z1 и избыточное давление Р1, скорость V1, а в сечении «2 - 2», соответственно z2 и Р2, V2.. Уравнение Бернулли для сечений «1- 1» и "2 – 2": Σh – сумма потерь на трение по длине и в местных сопротивлениях, а также потерь на входе и выходе из трубопровода.
|
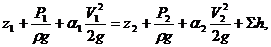(13.1)
