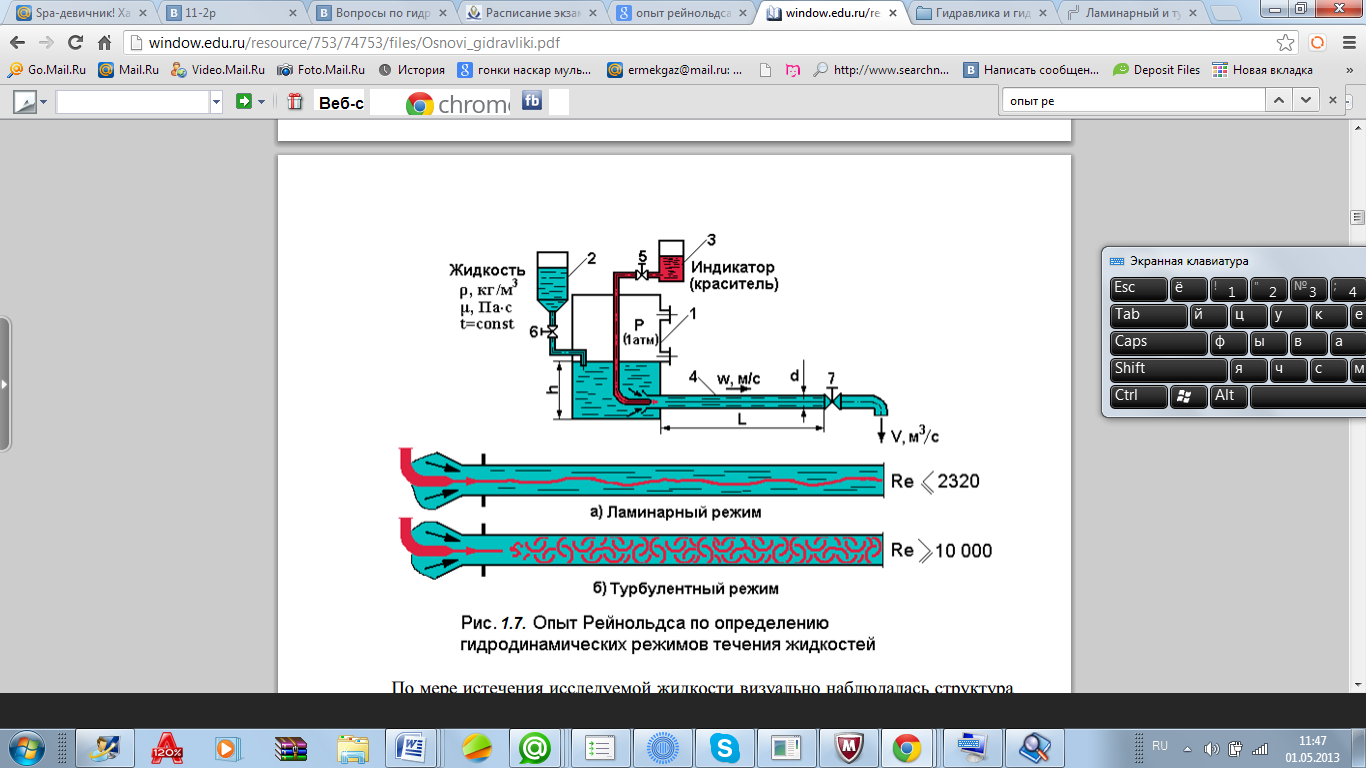
Опыт Рейнольдса.
Ламинарный и турбулентный режимы движения жидкости. Существуют два режима движения жидкости: ламинарный и турбулентный. При ламинарном режиме жидкость движется слоями без поперечного перемешивания, причем пульсации скорости и давления отсутствуют. При турбулентном режиме слоистость нарушается, движение жидкости сопровождается перемешиванием и пульсациями скорости и давления. Критерием для определения режима движения является безразмерное число Рейнольдса. Для труб круглого сечения число Рейнольдса определяется по формуле: Re = υ·d/ν; Режим будет ламинарным, если Re < Reкр;
и турбулентным, если Re > Reкр; числа Рейнольдса, для круглых труб обычно принимаемые равными соответственно 2320 и 580.
Опыт Рейнольдса. Опыт Рейнольдса состоял в следующем. Вначале при помощи крана 6 заполняли резервуар 1 жидкостью, а затем по достижении в нѐм уровня жидкости h, медленно открывался на определенный расход жидкости кран 7. После достижения стационарности потока жидкости в трубке 4, при помощи крана 5 по оси трубки 4 вводился индикатор из резервуара 3. По мере истечения исследуемой жидкости визуально наблюдалась структура потока жидкости в трубке 4 по поведению тонкой струйки индикатора. Проведенные опыты показали, что при скоростях жидкости меньше некоторого критического значения wкр струйка красителя, проходя по всей длине трубки 4, не размывалась и не смешивалась с жидкостью по всему сечению. При скоростях же превышающих это критическое значение w> wкр струйка индикатора, попадая в поток жидкости, начинала смешиваться с ней, заполняя всѐ сечение трубки. И чем выше было значение скорости, тем более интенсивным наблюдалось перемешивание. Очевидно, что в первом случае, когда индикатор не размывался, жидкость двигалась слоями параллельно стенкам трубы. Течение напоминало параллельно-струйчатое или слоистое движение, которое было названо ламинарным. Во втором случае, когда при скорости потока превышающей некоторый критический порог, несмотря на продолжающееся поступательное движение жидкости по трубе, наблюдалась такая картина: на некотором участке от ввода индикатора, последний вначале не смешивался с потоком жидкости, а затем наблюдалось образование завихрений, и индикатор перемешивался с жидкостью. Такое движение было названо турбулентным. Рейнольдсом было установлено, что переход от ламинарного к турбулентному режиму определяется с одной стороны физическими свойствами жидкости (ρ и μ), а с другой – скоростью течения w и диаметром 26 трубки d. На основании многочисленных экспериментов с различными жидкостями и трубками, при различных скоростях течения в результате обработки результатов опытов Рейнольдсом было установлено, что установленные режимы течения проявляются только при определенном соотношении указанных параметров. Рейнольдсом был сформирован безразмерный комплекс величин, который впоследствии был назван в честь Потери напора по длине, иначе их называют потерями напора на трение
где При равномерном движении жидкости на участке трубопровода постоянного диаметра d длиной l этот коэффициент сопротивления прямо пропорционален длине и обратно пропорционален диаметру трубы
где l – коэффициент гидравлического трения ( иначе его называют коэффициент потерь на трение или коэффициент сопротивления трения). Потери напора по длине определяются по формуле Дарси – Вейсбаха: здесь λ – коэффициент гидравлического сопротивления, L – длина трубопровода, Rг = ω/χ– гидравлический радиус, v – средняя скорость движения жидкости, g – ускорение свободного падения, ω - площадь живого сечения потока, χ - смоченный периметр. Коэффициент гидравлического сопротивления λ зависит от режима течения жидкости и шероховатости внутренней поверхности трубы (канала), т.е. λ = λ(Re, Δ/4Rг), Re = 4vRг/ν - число Рейнольдса, Δ/4Rг – относительная шероховатость, Δ – абсолютная шероховатость, ν – кинематическая вязкость. Средняя скорость движения жидкости может быть определена следующим образом v=Q/S, Q – объемный расход, S – площадь поперечного сечения потока.
Местными гидравлическими сопротивлениями называются любые участки гидравлической системы, где имеются повороты, преграды на пути потока рабочей жидкости, расширения или сужения, вызывающие внезапное изменение формы потока, скорости или направления ее движения. В этих местах интенсивно теряется напор. Примерами местных сопротивлений могут быть искривления оси трубопровода, изменения проходных сечений любых гидравлических аппаратов, стыки трубопроводов и т.п. Потери напора на местных сопротивлениях
где
|

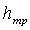 , в чистом виде, т.е. так, что нет никаких других потерь, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят и в шероховатых трубах, и в гладких. Величина этих потерь выражается зависимостью
, в чистом виде, т.е. так, что нет никаких других потерь, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят и в шероховатых трубах, и в гладких. Величина этих потерь выражается зависимостью ,
, - коэффициент сопротивления, обусловленный трением по длине.
- коэффициент сопротивления, обусловленный трением по длине. ,
,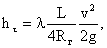 (1)
(1)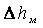 определяются по формуле Вейсбаха:
определяются по формуле Вейсбаха: ;
; - коэффициент местного сопротивления.
- коэффициент местного сопротивления.


