Определение параметров кинетики измельчения
Параметрами для определения кинетики измельчения угля являются: время измельчения проб угля и остатки его на ситах после рассева соответствующих проб. После обработки входных данных получается график зависимости суммарного остатка на сите от времени помола. Для определения данной зависимости был применен метод наименьших квадратов. За переменную х берется время измельчения определенной пробы, за у – масса остатка на конкретном сите определенной пробы. Далее для нахождения общей массы остатка на определенном сите суммируем массы остатков на ситах, которые крупнее данного сита. Таким образом, мы получаем массу остатка такую, если бы проводили ситовой анализ только с одним ситом. Затем с помощью уравнений регрессии методом наименьших квадратов решаем поставленную задачу. Можно использовать следующий вид уравнений регрессии:
Далее рассмотрим метод наименьших квадратов с линейной и нелинейной (параболической) регрессией. 1. Линейная регрессия Допустим, что имеем линейную парную корреляцию, которая выражается функцией (3.3), где а и b – неизвестные параметры. Для нахождения параметров а и b исследуем на минимум сумму квадратов разности функций
По правилу необходимого условия экстремума функции двух переменных находим частные производные по а и b и приравняем их нулю:
Выполнив преобразования с суммой, получим:
Разделив все члены системы (3.9) на n, получим:
Решив систему (3.10) относительно а и b, получим:
где Тогда уравнение (3.3) можно записать в виде:
Уравнение (3.12) называют уравнением регрессии у по х. 2. Нелинейная регрессия Допустим, что имеем параболическую парную регрессию, которая выражается функцией:
где а 0, а 1, а 2 – неизвестные параметры. Для нахождения параметров а 0, а 1, а 2 воспользуемся методом наименьших квадратов:
Далее находим частные производные по всем параметрам а 0, а 1, а 2 и приравняем их нулю:
Выполнив преобразования с суммами (3.15), получим:
Тогда получим уравнение в виде:
где Средняя квадратическая ошибка уравнения параболической регрессии находится по формуле:
Аналогично метод наименьших квадратов применяется и для других видов уравнений регрессии. При сравнении с помощью кубического уравнения регрессии получилось наименьшее среднеквадратическое отклонение.
|

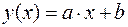 ; (3.3)
; (3.3) ; (3.4)
; (3.4)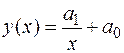 ; (3.5)
; (3.5)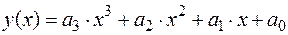 . (3.6)
. (3.6) и
и 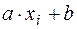 , т.е.
, т.е.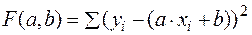 . (3.7)
. (3.7)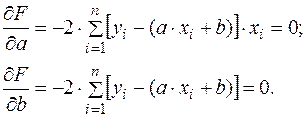 (3.8);
(3.8);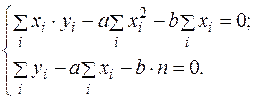 (3.9)
(3.9)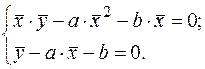 (3.10)
(3.10)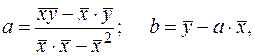 (3.11)
(3.11)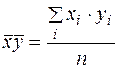 ,
,  ,
, 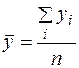 ,
, 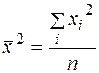 ,
,  .
. . (3.12)
. (3.12)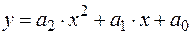 , (3.13)
, (3.13)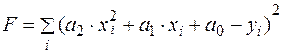 . (3.14)
. (3.14)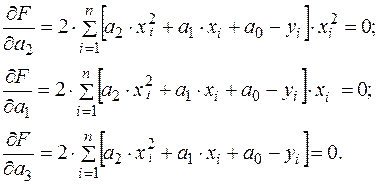 (3.15)
(3.15) (3.16)
(3.16)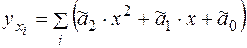 , (3.17)
, (3.17) – значения, вычисленные из системы (3.16).
– значения, вычисленные из системы (3.16). . (3.18)
. (3.18)


