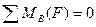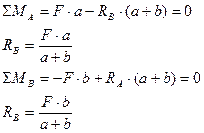Приклад 1
Таблиця 1 Структура заняття
6 Питання до семінарського заняття
1 Сила як фактор взаємодії тіл. Її характеристики, одиниця виміру. 2 Система сил. Рівнодійна сила. Врівноважуюча сила. 3 Пара сил. Ефект дії пари сил. Момент пари сил. Одиниця виміру моменту. 4 Момент сили відносно точки. Одиниця виміру моменту. 5 Балочні системи. Опори. Види навантажень балок. 6 Умови рівноваги плоскої системи довільно розташованих сил.
Питання для фронтального опитування 1 Мірою чого є сила? 2 Дайте визначення одиниці виміру сили. 3 Якими чинниками визначається ефект дії сили? 4 Яку дію здійснює сила на тіло?

6 Накресліть вектор сили тяжіння, який дорівнює 50Н, прийнявши, що масштаб зображення 10 мм відповідають 10Н. 7 Яку систему сил утворюють дві сили, лінії дії яких перпендикулярні між собою? 8 Дайте визначення рівнодійної сили. 9 Дайте ознаку врівноважуючої сили. 10 Як взаємно розташовані рівнодійна та врівноважуюча сили? 11 Чому стане еквівалентна система сил, якщо до неї додати врівноважуючу силу? 12 Чому дорівнює проекція вектора на вісь? 13 Вкажіть напрямок осі Х, при якому проекція вектора
14 При якому значенні кута 14.1 14.2 14.3
15 Дайте визначення, чому дорівнює момент сили відносно точки? 16 Як визначається плече сили відносно точки? 17 Визначте момент сили відносно точки А
18 Сформулюйте умови рівноваги плоскої системи довільно розташованих сил. 19 Перелічіть види навантажень балки. 20 Перелічіть види опор балочних систем. 21 Вкажіть, як направлені реакції в опорах балок?
8 Основні теоретичні відомості
Плоска система довільно розташованих сил еквівалентна одній силі (яка називається головним вектором) і одній парі (момент якої називається головним моментом) і прагне придати тілу в загальному випадку прямолінійний і обертальний рух одночасно. Плоска система збіжних сил та система пар являються окремими випадками довільної системи сил. Рівновага тіла буде тоді коли дорівнюють нулю головний вектор та головний момент системи. Аналітичною умовою рівноваги являється рівняння нулю алгебраїчних сум проекцій сил системи на любі дві взаємно перпендикулярні осі та алгебраїчної суми моментів відносно любої точки. При розв’язанні задач даного типу потрібно знати, що для балочних систем найчастіше використовується такі опори, як шарнірно- рухома та шарнірно - нерухома.
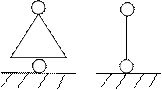
а) б) в)
Малюнок 1 Типи опор а) шарнірно-рухома; б) шарнірно-нерухома; в) жорстка закладка
В опорах з’являються реакції:
Малюнок 2 Реакції в опорах а) в шарнірно-рухомій; б) в шарнірно-нерухомій; в)в жорсткій закладці.
При виборі системи координат треба звернути увагу на раціональний вибір координатних осей та положення центру моментів. Початок відліку системи координат суміщають з однією з опор, що спрощує рішення. При розв’язанні задач одного типу треба мати чітку уяву про визначення проекцій сили на осі та про момент сили відносно точки.
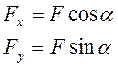
а) б) Малюнок 3 Проекції вектора на вісь
Знак проекції: якщо вектор та вісь направлені в один бік, то проекція має знак (+), якщо мають протилежні напрямки, то знак (-).
Малюнок 4 Момент сили відносно точки
де h – плече сили h – це перпендикуляр із т. А на лінію дії сили.
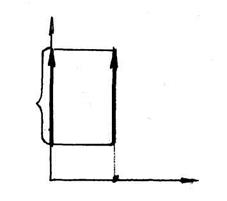
Малюнок 7 Приклад навантаження балки моментом пари сил Момент пари сил в рівняннях проекцій участі не приймає. Для розподіленого навантаження,
Малюнок 5 Навантаження балки розподіленим навантаженням де: q – інтенсивність розподіленого навантаження, Н/м Q – рівнодійна розподіленого навантаження, прикладена в його центрі ваги.
Приклад навантаженої балки
Малюнок 8 Балка, яка навантажена плоскою системою довільно розташованих сил.
Алгоритм рішення задач на систему довільно розташованих сил 1 Вибираємо раціональну систему координат. 2 Вибираємо об’єкт рівноваги – балка. 3 Відкинемо зв’язки та замінимо їх дію реакціями зв’язків. 4 Вибираємо раціональну систему координат та складаємо розрахункову схему. 5 Запишемо умови рівноваги та складемо рівняння:
6 Розв’язуємо ці рівняння відносно невідомих. Визначаємо опорні реакції. 7 Виконуємо перевірку. Для перевірки використовуємо одне із рівнянь рівноваги. 10 Розв’язання типових задач
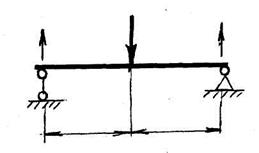
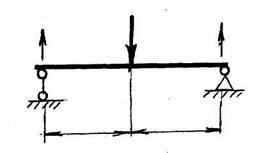
Завдання Визначити опорні реакції балки
Приклад 1
Рішення
1 Об’єкт рівноваги – балка. 2 Відкинемо зв’язки та замінимо їх дію реакціями зв’язків. 3 Вибираємо раціональну систему координат та складаємо розрахункову схему:
4 Запишемо та складемо рівняння рівноваги:
Перевірка
|

 на вісь Х буде позитивною
на вісь Х буде позитивною
 між силою та віссю проекція сили дорівнює нулю
між силою та віссю проекція сили дорівнює нулю





 б)
б) 
 в)
в) 

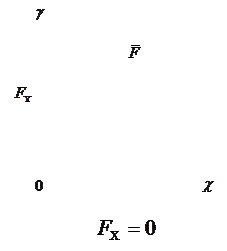






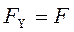
 а)
а) 
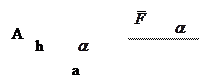 Момент сили відносно точки
Момент сили відносно точки
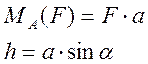
 Момент пари сил
Момент пари сил



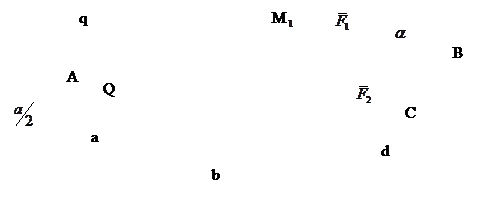



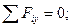



 ;
;  ;
;