Метод пробних ділень
На цій теоремі базується також метод пробних ділень, або метод Леонардо Фібоначчі. Опишемо алгоритм цього метода. Для того, щоб визначити, простим чи складеним є число n, необхідно: 1. Знайти 2. Виписати всі прості числа, які не перевищують 3. Перевірити, чи ділиться n на виписані прості числа. Якщо n ділиться хоча б на одне з виписаних простих чисел, то n буде складеним, якщо не ділиться – простим. Приклад 2. Визначити, простим чи складеним є число: а) 247; б) 397. а) Знаходимо 247: 13 = 19, отже, число 247 = 13 × 19 – складене. б) 2, 3, 5, 7, 11, 13, 17, 19. Число 397 не ділиться на жодне з виписаних простих чисел, тому воно просте. Теорема (Основна теорема аріфметики). Кожне, відмінне від 1, натуральне число n можна записати у вигляді добутку простих чисел єдиним способом, якщо не брати до уваги порядку розміщення співмножників. Ця теорема показує, що всі натуральні числа, відмінні від 1, дістають з простих чисел за допомогою операції множення. Кожне складене натуральне число є деяким добутком простих чисел, причому різні добутки дають різні числа. У розкладі n = р 1× р 2×…× рs (2) натурального числа n на прості множники р 1, р 2,…, рs деякі з цих множників можуть повторюватись. Якщо простий множник рі повторюється у розкладі k раз, то його називають k -кратним множником числа n, або кажуть, що множник рі має кратність k. Позначимо символами р 1, р 2, …, рm (m Î N) попарно різні множники у розкладі (2). Нехай множник рі (і = 1,…, m) має відповідну кратність ki. Тоді розклад числа n у добуток простих множників можна записати так: n = р 1 k1 × р 2 k2 ×…× рm km , де ki >0, і = 1,…, m. Цей запис називають канонічним розкладом числа n на прості множники. Канонічний запис натурального числа єдиний. Процес розкладу числа на прості множники називають факторизацією. Приклад 1. Знайти канонічний розклад числа12600, 3887. а) Застосуємо ознаки подільності: 12600 = 126×100 = 2×63×25×4 = 2×32×52 ×22 = 23×32×52×7. б) Дане число не має малих дільників (2,3,5,7), тому використаємо метод пробних ділень:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 49, 53, 59,61; 3887=13×299
2, 3, 5, 7, 11, 13, 17 3887=13×299=13∙13∙23= 132∙23. Наслідок. Якщо натуральні числа а і b, відмінні від 1, записано в формі а = р 1 k 1 ×р 2 k 2 ×…×рm km, ki ≥0, b = р 1 t 1× р 2 t 2×…× рmtm, ti ≥0, то а Цей наслідок іноді називають загальною ознакою подільності натуральних чисел.
|

 .
.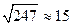 і виписуємо всі прості числа, які не перевищують 15: 2, 3, 5, 7, 11, 13.
і виписуємо всі прості числа, які не перевищують 15: 2, 3, 5, 7, 11, 13.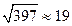 , виписуємо всі прості числа до 19 включно:
, виписуємо всі прості числа до 19 включно: »62;
»62;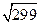 » 17
» 17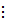 b тоді і тільки тоді, коли ki ≥ ti, і = 1,…, m.
b тоді і тільки тоді, коли ki ≥ ti, і = 1,…, m.


