Решето Ератосфена
Задача: Виписати всі прості числа від 2 до N=30. Випишемо усі натуральні числа від 2 до 30: 2,3,4,…,30. (1) Перше число у цьому ряду – 2. Це число просте. Закреслимо у ряду (1) всі числа, кратні 2, крім самого числа 2, тобто кожне друге після 2. Першим не закресленим числом після 2 у ряді (1) є число 3. Число 3 не ділиться на 2, бо в іншому випадку ми б закреслили його: отже, число 3 ділиться лише на 1 і самого себе, тому воно просте. Закреслимо тепер у ряді (1) всі числа, кратні 3, крім самого числа 3, тобто кожне третє після 3.
Уперше для складання таблиць простих чисел описаний щойно метод застосував грецький математик Ератосфен. Він писав числа на папірусі, натягнутому на рамку, числа він не закреслював, а проколював. Внаслідок цього він дістав дещо схоже на решето: складені числа «просіювались» крізь це решето, а прості числа залишались. Тому цей метод називають решетом Ератосфена. Математичні підстави цього метода базуються на наступній теоремі:
|
Першим не закресленим числом після 3 є число 5; воно не ділиться ні на 2, ні на 3, бо в іншому випадку воно виявилось б закресленим; отже, 5 ділиться тільки на 1 і на самого себе, тому воно просте число. У ряду (1) закреслимо всі числа, кратні 5, крім самого числа 5, тобто кожне п’яте після 5, і т.д. Закресливши в ряду (1) всі числа, кратні простим числам, не більшим ніж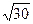
, дістанемо таблицю всіх простих чисел, які не перевищують числа 30.
