Число натуральних дільників даного n Î NФункція t(n) визначена при всіх натуральних n і її значення дорівнює числу всіх натуральних дільників числа n. Теорема. t(n) = (a1 + 1)(a2 + 1)…(am + 1), де a1, a2, …, am – показники степенів простих дільників у канонічному розкладі числа Наслідок 2. Функція t(n) мультиплікативна. Приклад 3. Знайти число всіх натуральних дільників числа 360. Знаходимо канонічний розклад числа 360=23 × 32 × 51, тоді t(360) = (3 + 1)(2 + 1)(1 + 1) = 24. Функція Ейлера j(n) визначена для всіх n Î N, її значення дорівнює кількості натуральних чисел взаємно простих з числом n, які не перебільшують n. Доведемо основні властивості цієї функції: Властивість 1. j(1) = 1. Властивість 2. j(р) = р – 1, якщо р – просте. Властивість 3. j(рk) = рk-1 (р – 1), якщо р – просте. Властивість 4. j(а×b) = j(а) × j(b), якщо (а, b)=1. Теорема. Приклад 1. Обчислити функцію Ейлера для чисел 17; 720. 1) n =17 – просте, тому використовуємо властивість (2): j(17)= 17 – 1= 16. 2) n =720 – складене, 720 = 24 × 32 × 5. j(720) = j(24 × 32 × 5) = j(24) × j(32) × j(5) = 24-1 × (2 – 1) × 32-1 × (3 – 1) × (5 – 1) = 23 × 1 × 3 × 2 × 4 = 192. Приклад 2. Знайти натуральне число n, якщо j(n) = 3600 і n = 3 k × 5 m × 7s, де k, m, s Î N. Обчислимо: j(n)=j(3 k ×5 m ×7 s)=j(3 k)×j(5 m)×j(7 s) = 3 k- 1× 2× 5 m- 1×4 × 7 s- 1∙6. Маємо рівняння: 3 k- 1 × 2 × 5 m- 1×4 × 7 s -1× 6 = 3600. 3 k -1 × 5 m -1 × 7 s -1= 75 = 3 × 52, звідки k – 1 = 1, m – 1 = 2, s – 1 = 0; k = 2, m = 3, s = 1. Шукане число n = 32 × 53 × 71 = 7875.
|
Наслідок 1. Якщо р – просте, то t(p)=2.
, де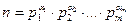 
– канонічний розклад числа.
