Теорія порівнянь
Означення. Цілі числа а і b називають порівнянними (конгруентними) за модулем m, m – натуральне число, відмінне від 1, якщо (а – b) Символично це відношення записується так: «а º b (mod m)» і читається: «а порівнянно з b за модулем m». Приклад 1. Які з чисел а, b, c порівнянні з числом d = 11 за модулем m, якщо а = 217, b = 201, c = 186, m = 19? Складемо відповідні порівняння і перевіримо, чи є вони вірними: 1) 217 º 11(mod 19). За означенням, знаходимо різницю чисел 217 і 11 і перевіряємо, чи ділиться вона на 19. (217 – 11) = 206 2) 201 º 11(mod 19). (201 – 11) = 190 3) 186 º 11(mod 19). (186 – 11) = 175 Теорема. a º r (mod m), де a = mq + r, де 0 £ r < m. Якщо а º b (mod m), то число (a – b) кратне числу m, звідки а – b = mt, t Î Z, або а = b + mt, t Î Z. З іншого боку, " a Î Z a = mq + r, де 0 £ r < m. Тоді a – r = mq і a º r (mod m). Критерій порівнянності чисел. Цілі числа порівнянні за модулем m тоді і тільки тоді, коли вони дають однакові остачі при діленні на m. Приклад 2. Записати у вигляді порівнянь умови: 1) при діленні на 8 число 53 дає остачу 5; 2) числа 219 і 129 дають неоднакові остачі при діленні на 7; 3) n = 7 k + 3, k Î Z; 4) n – парне. 1) 53 = 8 t + 5, звідки 53 º 5(mod 8); 2) 219 3) n º 3(mod 7); 4) n = 2 k, k Î Z, тому n º 0(mod 2).
|
.
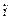19, тому 217 
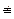11(mod 19);
19, тому 201 º 11(mod 19);
