Серьезной проблемой при построении моделей множественной линейной регрессии по МНК является мультиколлинеарность — линейная взаимосвязь двух или нескольких объясняющих переменных. Если объясняющие переменные связаны строгой функциональной зависимостью, то говорят о совершенной мультиколлинеарности. В случае совершенной мультиколлинеарности матрица 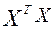 оказывается вырожденной, т.е. ее определитель равен нулю, а значит, не существует обратная матрица
оказывается вырожденной, т.е. ее определитель равен нулю, а значит, не существует обратная матрица 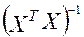 , которая участвует в основных соотношениях метода наименьших квадратов.
, которая участвует в основных соотношениях метода наименьших квадратов.
Совершенная мультиколлинеарность является скорее теоретическим примером. Реальна же ситуация, когда между объясняющими переменными существует довольно сильная корреляционная зависимость, а не строгая функциональная. Такая зависимость называется несовершенной мультиколлинеарностью. Мультиколлинеарность затрудняет разделение влияния объясняющих факторов на поведение зависимой переменной и делает оценки коэффициентов регрессии ненадежными.
Нестрогая линейная зависимость между объясняющими переменными необязательно дает неудовлетворительные оценки. Если число наблюдений и выборочные дисперсии объясняющих переменных велики, а дисперсия случайного члена мала, то в итоге можно получить вполне хорошие оценки. Оценка любой регрессии будет страдать от мультиколлинеарности в определенной степени, если только все независимые переменные не окажутся абсолютно некоррелированными. Рассмотрение данной проблемы начинается только тогда, когда это серьезно влияет на результаты оценки регрессии. Эта проблема является обычной для регрессий временных рядов, когда данные состоят из ряда наблюдений в течение какого-то периода времени. Если две или более объясняющие переменные имеют ярко выраженный временной тренд, то они будут тесно коррелированны, и это может привести к мультиколлинеарности.

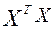 оказывается вырожденной, т.е. ее определитель равен нулю, а значит, не существует обратная матрица
оказывается вырожденной, т.е. ее определитель равен нулю, а значит, не существует обратная матрица 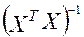 , которая участвует в основных соотношениях метода наименьших квадратов.
, которая участвует в основных соотношениях метода наименьших квадратов.


