Определение мультиколлинеарности
Точных количественных критериев для определения наличия (отсутствия) мультиколлинеарности не существует. Тем не менее, существуют некоторые рекомендации по выявлению мультиколлинеарности. 1. В первую очередь анализируют матрицу парных коэффициентов корреляции
точнее ту ее часть, которая относится к объясняющим переменным:
Здесь 2. Если определитель матрицы 3. Коэффициент детерминации 4. Высокие частные коэффициенты корреляции свидетельствуют о наличии мультиколлинеарности. При изучении многомерных связей необходимо измерять действительную силу линейной связи между двумя переменными, очищенную от влияния на рассматриваемую пару переменных других факторов. Частные коэффициенты корреляции определяют силу линейной зависимости между двумя переменными без учета влияния на них других переменных. Выборочный частный коэффициент корреляции между переменными Пусть
Тогда
При проверке статистически значимого отличия от нуля выборочного частного коэффициента корреляции и при построении для него доверительных интервалов следует пользоваться рекомендациями для парного коэффициента корреляции, но во всех формулах объем выборки полагать равным 5. Более внимательное изучение вопроса мультиколлинеарности производится следующим образом. Строятся уравнения регрессии каждой из объясняющих переменных
Здесь 6. О присутствии мультиколлинеарности сигнализируют некоторые внешние признаки модели: · некоторые из оценок коэффициентов имеют неправильные с точки зрения экономической теории знаки или неоправданно большие значения; · небольшое изменение исходных данных (добавление или изъятие небольшой порции наблюдений) приводит к существенному изменению оценок коэффициентов; · большинство или даже все оценки коэффициентов регрессии оказываются статистически незначимо отличающимися от нуля (при проверке с помощью
|

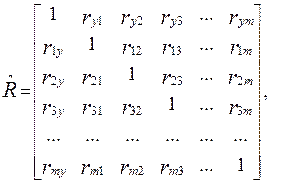 (50)
(50)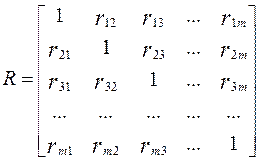 . (51)
. (51)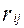 - парный коэффициент корреляции между переменными
- парный коэффициент корреляции между переменными 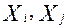 ;
; 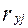 - парный коэффициент корреляции между
- парный коэффициент корреляции между  . Считается, что наличие коэффициентов
. Считается, что наличие коэффициентов 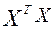 близок к нулю (например, одного порядка с накапливающимися ошибками вычислений), то это свидетельствует о наличии мультиколлинеарности.
близок к нулю (например, одного порядка с накапливающимися ошибками вычислений), то это свидетельствует о наличии мультиколлинеарности.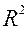 достаточно высок, но некоторые из коэффициентов регрессии статистически незначимы, т.е. они имеют низкие
достаточно высок, но некоторые из коэффициентов регрессии статистически незначимы, т.е. они имеют низкие 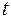 -статистики.
-статистики. очищенный от влияния остальных
очищенный от влияния остальных 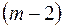 объясняющих переменных, символически обозначается
объясняющих переменных, символически обозначается 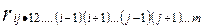 . Приведем формулу расчета данного коэффициента.
. Приведем формулу расчета данного коэффициента.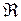 - матрица обратная к матрице
- матрица обратная к матрице 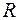 :
: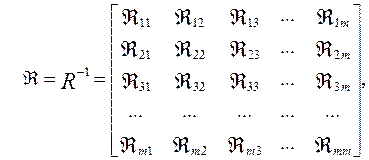 (52)
(52)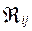 - алгебраическое дополнение к
- алгебраическое дополнение к 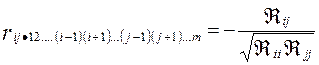 . (53)
. (53)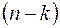 , где
, где 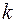 - остальные объясняющие переменные, т.е. переменные влияние которых исключается при расчете частных коэффициентов корреляции.
- остальные объясняющие переменные, т.е. переменные влияние которых исключается при расчете частных коэффициентов корреляции.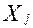 на оставшиеся объясняющие переменные
на оставшиеся объясняющие переменные 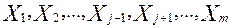 . Вычисляются коэффициенты детерминации
. Вычисляются коэффициенты детерминации 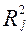 и рассчитывается их статистическая значимость на основе F -статистики:
и рассчитывается их статистическая значимость на основе F -статистики: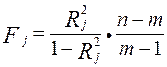 .
. — число наблюдений,
— число наблюдений, 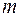 — число объясняющих переменных в первоначальном уравнении регрессии. Статистика
— число объясняющих переменных в первоначальном уравнении регрессии. Статистика 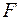 имеет распределение Фишера с
имеет распределение Фишера с 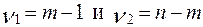 степенями свободы. Если коэффициент
степенями свободы. Если коэффициент 


